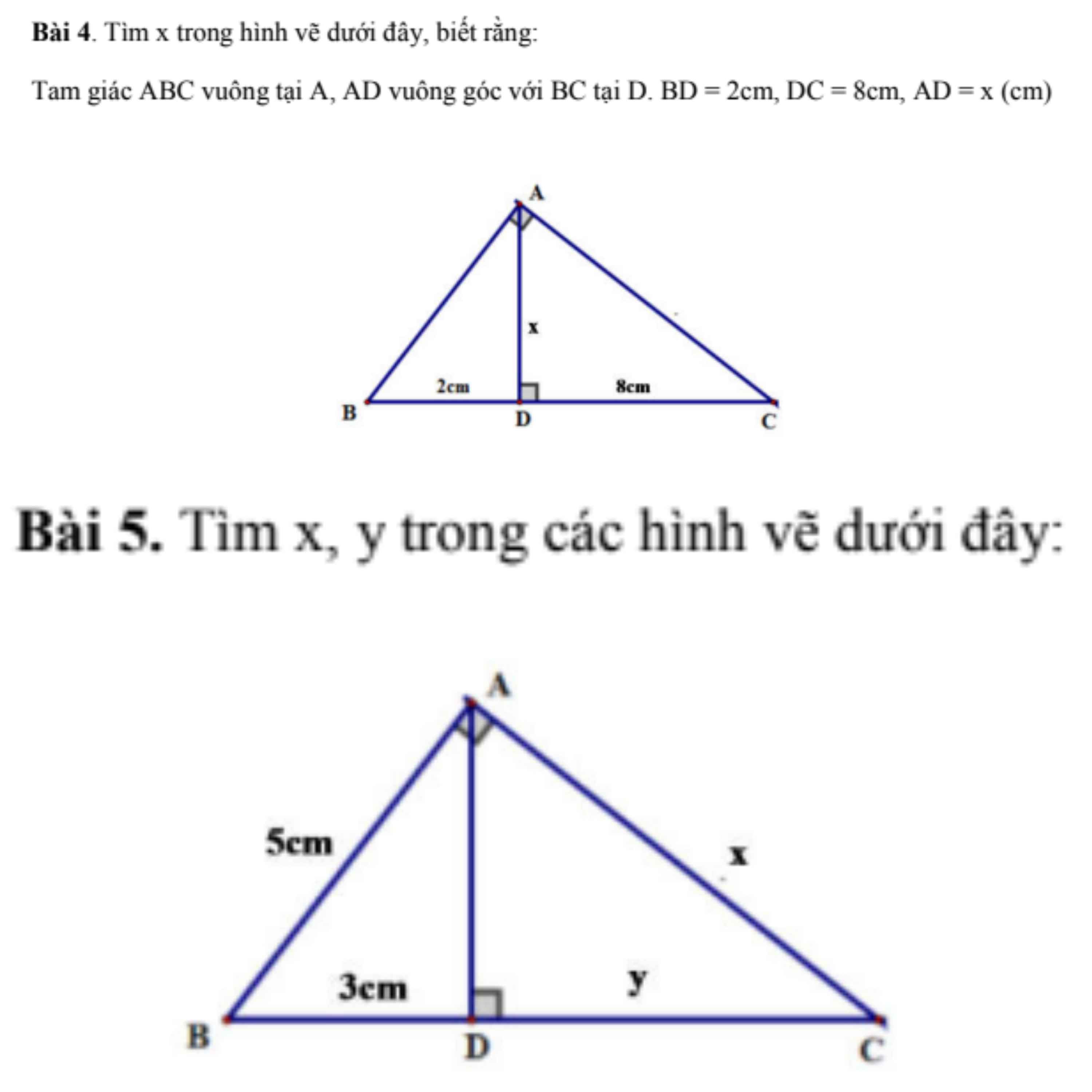
Bài `4:`
Xét `\triangle ABC` vuông tại `A` có: `AD` là đường cao
`=>AD^2=BD.DC` (Ht giữa cạnh và đường cao)
`=>x^2=2.8=16=>x=4(cm)`
_______________________________________________________
Bài `5:`
Xét `\triangle ABC` vuông tại `A` có: `AD` là đường cao
`=>AB^2=BD.BC` (Ht giữa cạnh và đường cao)
`=>5^2=3.BC=>BC=25/3(cm)`
Có: `BD+DC=BC`
`=>3+y=25/3=>y=16/3(cm)`
Xét `\triangle ABC` vuông tại `A` có: `AB^2+AC^2=BC^2`
`=>5^2+x^2=(25/3)^2`
`=>x=20/3(cm)`
Bài 4:
Áp dụng HTL vào tg ABC vuông tại A, có đường cao AD:
\(AD^2=BD^2\cdot DC^2\)
\(\Rightarrow AD=\sqrt{BD^2\cdot DC^2}=\sqrt{2^2\cdot8^2}=16\left(cm\right)\)
Bài 5:
Áp dụng Pytago vào tg ABD vuông tại D:
\(AB^2=AD^2+BD^2\)
\(\Rightarrow AD=\sqrt{AB^2-BD^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
Áp dụng HTL vào tg ABC vuông tại A, có đường cao AD:
\(\dfrac{1}{AD^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Rightarrow\dfrac{1}{AC}=\sqrt{\dfrac{1}{AD^2}-\dfrac{1}{AB^2}}=\sqrt{\dfrac{1}{4^2}-\dfrac{1}{5^2}}=\dfrac{3}{20}=\dfrac{20}{3}\left(cm\right)\)