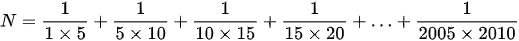\(N=\dfrac{1}{1.5}+\dfrac{1}{5.10}+\dfrac{1}{10.15}+\dfrac{1}{15.20}+...+\dfrac{1}{2005+2010}\)
\(N=\dfrac{1}{1.5}+\dfrac{1}{5}\left(\dfrac{5}{5.10}+\dfrac{5}{10.15}+\dfrac{5}{15.20}+...+\dfrac{5}{2005+2010}\right)\)
\(N=\dfrac{1}{5}+\dfrac{1}{5}\left(\dfrac{1}{5}-\dfrac{1}{10}+\dfrac{1}{0}-\dfrac{1}{15}+...+\dfrac{1}{2005}-\dfrac{1}{2010}\right)\)
\(N=\dfrac{1}{5}+\dfrac{1}{5}\left(\dfrac{1}{5}-\dfrac{1}{2010}\right)\)
\(N=\dfrac{1}{5}\left(1+\dfrac{1}{5}-\dfrac{1}{2010}\right)\)
\(N=\dfrac{1}{5}.\dfrac{2411}{2010}\)
\(N=\dfrac{2411}{10050}\)
\(N=2.\left(\dfrac{1}{1.5}+\dfrac{1}{5.10}+\dfrac{1}{10.15}+...+\dfrac{1}{2005.2010}\right)\)
\(2\)\(N=\dfrac{2}{1.5}+\dfrac{2}{5.10}+\dfrac{2}{10.15}+...+\dfrac{2}{2005.2010}\)
\(2\)\(N=\dfrac{1}{1}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{15}+...+\dfrac{1}{2005}-\dfrac{1}{2010}\)
\(2\)\(N=\dfrac{1}{1}-\dfrac{1}{2010}\)
\(2N=\dfrac{2009}{2010}\)
\(N=\dfrac{2009}{2010}:2\)
\(N=\dfrac{2009}{4020}\)
\(N=5.\left(\dfrac{1}{1x5}+\dfrac{1}{5x10}+\dfrac{1}{10x15}+\dfrac{1}{15x20}+....+\dfrac{1}{2005x2010}\right)\)
\(5N=\dfrac{1}{1x5}+\dfrac{1}{1x10}+\dfrac{1}{10x15}+\dfrac{1}{15x20}+......+\dfrac{1}{2005x2010}\)
\(5N=1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{15}+\dfrac{1}{15}-\dfrac{1}{20}+.....+\dfrac{1}{2005}-\dfrac{1}{2010}\)
\(5N=1-\dfrac{1}{2010}\)
\(5N=\dfrac{2009}{2010}\)
\(N=\dfrac{2009}{2010}:5\)
\(N=\dfrac{2009}{10050}\)
\(N=1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{15}+\dfrac{1}{15}-\dfrac{1}{20}+.....+\dfrac{1}{2005}-\dfrac{1}{2010}\)
\(N=1-\dfrac{1}{2010}\)
\(N=\dfrac{2009}{2010}\)