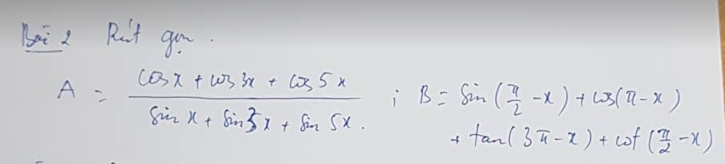\(A=\dfrac{cosx+cos3x+cos5x}{sinx+sin3x+sin5x}=\dfrac{cos5x+cosx+cos3x}{sin5x+sinx+sin3x}=\dfrac{2cos\dfrac{5x+x}{2}cos\dfrac{5x-x}{2}+cos3x}{2sin\dfrac{5x+x}{2}cos\dfrac{5x-x}{2}+sin3x}=\dfrac{2cos3x.cos2x+cos3x}{2sin3x.cos2x+sin3x}=\dfrac{cos3x\left(2cos2x+1\right)}{sin3x\left(2cos2x+1\right)}=\dfrac{cos3x}{sin3x}=cot3x\)
\(B=sin\left(\dfrac{\pi}{2}-x\right)+cos\left(\pi-x\right)+tan\left(3\pi-x\right)+cot\left(\dfrac{\pi}{2}-x\right)=cosx-cosx-tanx+tanx=0\)
Đúng 1
Bình luận (0)
