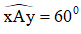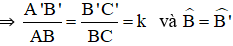refer
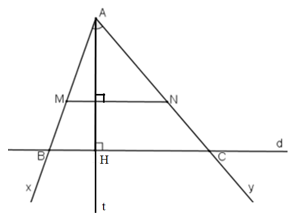
* Cách dựng:
+ Dựng góc 
+ Trên tia Ax lấy điểm M sao cho AM = 4; trên tia Ay lấy điểm N sao cho AN = 5.
+ Kẻ tia At vuông góc với MN
+ Trên tia At lấy điểm H sao cho AH = 6cm.
+ Kẻ đường thẳng d qua H và vuông góc với At cắt Ax và Ay lần lượt tại B và C.
Ta được tam giác ABC cần dựng.
* Chứng minh :
Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.
ΔABC dựng được có AH ⊥ BC ; AH = 6 và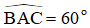 
;
Lại có AH ⊥ BC, MN ⊥ AH ⇒ MN // BC
⇒ ΔAMN 
ΔABC
Suy ra: 
(tính chất hai tam giác đồng dạng).
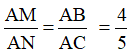
Vậy tam giác ABC dựng được thỏa mãn yêu cầu đề bài.
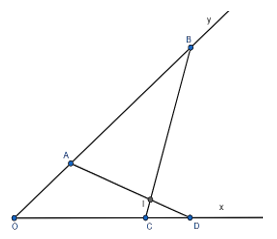
bài 32:
a) Ta có:
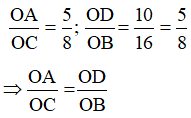
Xét ∆OCB và ∆OAD có:
∠O chung
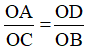
Suy ra: ∆OCB ∆OAD (c.g.c).
b) Xét ∆ICD và ∆IAB có:
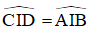(đối đỉnh)
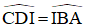(hai góc tương ứng của hai tam giác đồng dạng ∆OCB ∆OAD).
⇒ 
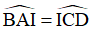(tính chất tổng ba góc trong một tam giác)
Vậy hai tam giác ICD và IAB có các góc bằng nhau từng đôi một.
’
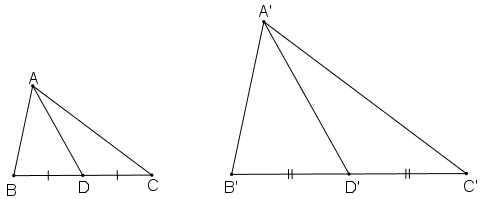
bài 33:
Giả sử ΔA’B’C’ ΔABC theo tỉ số k
Gọi D, D’ lần lượt là trung điểm BC và B’C’.
bài 34:
* Cách dựng:
+ Dựng góc
+ Trên tia Ax lấy điểm M sao cho AM = 4; trên tia Ay lấy điểm N sao cho AN = 5.
+ Kẻ tia At vuông góc với MN
+ Trên tia At lấy điểm H sao cho AH = 6cm.
+ Kẻ đường thẳng d qua H và vuông góc với At cắt Ax và Ay lần lượt tại B và C.
Ta được tam giác ABC cần dựng.
* Chứng minh :
Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.
ΔABC dựng được có AH ⊥ BC ; AH = 6 và ;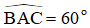
Lại có AH ⊥ BC, MN ⊥ AH ⇒ MN // BC
⇒ ΔAMN ΔABC
Suy ra: (tính chất hai tam giác đồng dạng).
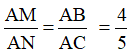
Vậy tam giác ABC dựng được thỏa mãn yêu cầu đề bài.
