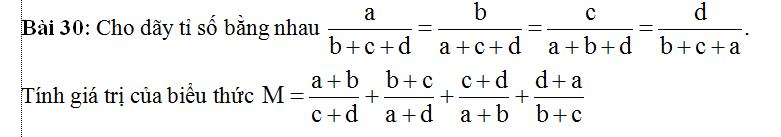-Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\dfrac{a}{b+c+d}=\dfrac{b}{a+c+d}=\dfrac{c}{a+b+d}=\dfrac{d}{b+c+a}=\dfrac{a+b+c+d}{b+c+d+a+c+d+a+b+d+b+c+a}=\dfrac{a+b+c+d}{4\left(a+b+c+d\right)}=\dfrac{1}{4}\)
\(\Rightarrow\dfrac{a}{b+c+d}=\dfrac{1}{4}\Rightarrow4a=b+c+d\Rightarrow5a=a+b+c+d\) (1)
\(\Rightarrow\dfrac{b}{a+c+d}=\dfrac{1}{4}\Rightarrow4b=a+c+d\Rightarrow5b=a+b+c+d\) (2)
\(\Rightarrow\dfrac{c}{a+b+d}=\dfrac{1}{4}\Rightarrow4c=a+b+d\Rightarrow5c=a+b+c+d\) (3)
\(\Rightarrow\dfrac{d}{b+c+a}=\dfrac{1}{4}\Rightarrow4d=b+c+a\Rightarrow5d=a+b+c+d\)
-Từ (1), (2), (3), (4) suy ra: \(4a=4b=4c=4d\Rightarrow a=b=c=d\)
\(M=\dfrac{a+b}{c+d}+\dfrac{b+c}{d+a}+\dfrac{c+d}{a+b}+\dfrac{d+a}{b+c}=\dfrac{a+a}{a+a}+\dfrac{a+a}{a+a}+\dfrac{a+a}{a+a}+\dfrac{a+a}{a+a}=1+1+1+1=4\)