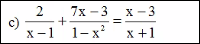\(\dfrac{2}{x-1}+\dfrac{7x-3}{1-x^2}=\dfrac{x-3}{x+1}\) (đk: \(x\ne\pm1\) )
\(\Leftrightarrow\dfrac{2}{x-1}-\dfrac{7x-3}{x^2-1}-\dfrac{x-3}{x+1}=0\)
\(\Leftrightarrow\dfrac{2\left(x+1\right)-7x+3-\left(x-3\right)\left(x-1\right)}{x^2-1}=0\)
\(\Leftrightarrow2x+2-7x+3-x^2+x+3x-3=0\)
\(\Leftrightarrow-x^2-x+2=0\)
\(\Delta=b^2-4ac=\left(-1\right)^2-4.\left(-1\right).2=9>0\Rightarrow\sqrt{\Delta}=3\)
\(\left\{{}\begin{matrix}x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{1+3}{-2}=-2\left(n\right)\\x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{1-3}{-2}=1\left(l\right)\end{matrix}\right.\)
Vậy \(S=\left\{-2\right\}\)
Đúng 0
Bình luận (0)
