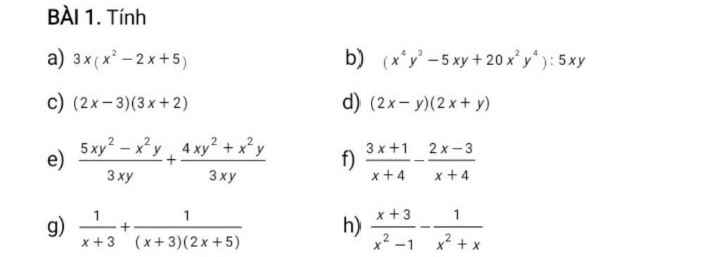a)=3x3-6x215x
b)=0,2x3y-1+4xy3
c)=6x2+4x-9x-6=6x2-5x-6
d)=4x2-y2
\(a,3x\left(x^2-2x+5\right)=3x^3-6x^2+15x\\ b,\left(x^4y^2-5xy+20x^2y^4\right):5xy=\dfrac{1}{5}x^3y-1+4xy^3\\ c,\left(2x-3\right)\left(3x+2\right)=6x^2-9x+4x-6=6x^2-5x-6\\ d,\left(2x-y\right)\left(2x+y\right)=4x^2-y^2\\ e,\dfrac{5xy^2-x^2y}{3xy}+\dfrac{4xy^2+x^2y}{3xy}=\dfrac{5xy^2-x^2y+4xy^2+x^2y}{3xy}=\dfrac{9xy^2}{3xy}=3y\)
\(f,\dfrac{3x+1}{x+4}-\dfrac{2x-3}{x+4}=\dfrac{3x+1-2x+3}{x+4}=\dfrac{x+4}{x+4}=1\\ g,\dfrac{1}{x+3}+\dfrac{1}{\left(x+3\right)\left(2x+5\right)}=\dfrac{2x+5}{\left(x+3\right)\left(2x+5\right)}+\dfrac{1}{\left(x+3\right)\left(2x+5\right)}=\dfrac{2x+5+1}{\left(x+3\right)\left(2x+5\right)}=\dfrac{2x+6}{\left(x+3\right)\left(2x+5\right)}=\dfrac{2\left(x+3\right)}{\left(x+3\right)\left(2x+5\right)}=\dfrac{2}{2x+5}\)
\(h,\dfrac{x+3}{x^2-1}-\dfrac{1}{x^2+x}=\dfrac{x+3}{\left(x-1\right)\left(x+1\right)}-\dfrac{1}{x\left(x+1\right)}=\dfrac{x\left(x+3\right)}{x\left(x-1\right)\left(x+1\right)}-\dfrac{x-1}{x\left(x-1\right)\left(x+1\right)}=\dfrac{x^2+3x}{x\left(x-1\right)\left(x+1\right)}-\dfrac{x-1}{x\left(x-1\right)\left(x+1\right)}=\dfrac{x^2+3x-x+1}{x\left(x-1\right)\left(x+1\right)}=\dfrac{x^2+2x+1}{x\left(x-1\right)\left(x+1\right)}=\dfrac{\left(x+1\right)^2}{x\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{x\left(x-1\right)}\)