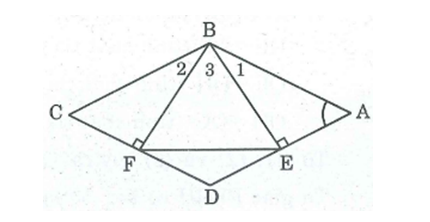
Xét hai tam giác vuông BEA và BFC, ta có:
∠∠(BEA) = ∠∠(BFC) = 900900
∠∠A = ∠∠C (tính chất hình thoi)
BA = BC (gt)
Suy ra: Δ∆BEA = Δ∆BFC (cạnh huyền, góc nhọn)
Do đó, ta có:
* BE = BF ⇒ ΔBEF cân tại B
* ∠∠B1B1 = ∠∠B2B2
Trong tam giác vuông BEA, ta có:
∠∠A + ∠∠B1= 900900 ⇒ ∠∠B1= 900900 – ∠∠A = 900−600=300900-600=300
⇒ ∠∠B2B2= ∠∠B1B1 = 300300
∠∠A + ∠∠(ABC) = 18001800 (hai góc trong cùng phía bù nhau)
⇒ ∠∠(ABC) = 18001800 – ∠∠A = 1800−600=12001800-600=1200
⇒ ∠∠(ABC) = ∠∠B1B1+ ∠∠B2B2+ ∠∠B3B3
⇒∠∠B3B3 = ∠∠(ABC) – (∠∠B1B1 + ∠∠B2B2) = 1200−(300+300)=6001200-300+300=600
Tam giác BEF cân tại B có ∠∠(EBF) = 600600 nên Δ∆BEF đều.
Đúng 1
Bình luận (2)
