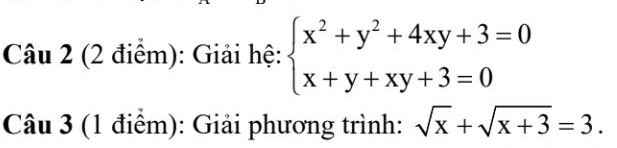Câu 2:
Đặt \(\left\{{}\begin{matrix}a=x+y\\b=xy\end{matrix}\right.\)
\(HPT\Leftrightarrow\left\{{}\begin{matrix}a^2+2b+3=0\\a+b+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a^2+2b+3=0\\2a+2b+6=0\end{matrix}\right.\Leftrightarrow a^2-2a-3=0\\ \Leftrightarrow\left[{}\begin{matrix}a=3\Rightarrow b=-6\\a=-1\Rightarrow b=-2\end{matrix}\right.\)
Với \(a=3;b=-6\Leftrightarrow\left\{{}\begin{matrix}x+y=3\\xy=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3-y\\y^2-3y-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=\dfrac{3-\sqrt{33}}{2}\\y=\dfrac{3+\sqrt{33}}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}x=\dfrac{3+\sqrt{33}}{2}\\y=\dfrac{3-\sqrt{33}}{2}\end{matrix}\right.\end{matrix}\right.\)
Với \(a=-1;b=-2\Leftrightarrow\left\{{}\begin{matrix}x+y=-1\\xy=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-y-1\\y^2+y-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=-2\\y=1\end{matrix}\right.\\\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\end{matrix}\right.\)
Vậy HPT có nghiệm ...
Câu 3:
\(ĐK:x\ge0\\ PT\Leftrightarrow\sqrt{x+3}=3-\sqrt{x}\\ \Leftrightarrow x+3=x+9-6\sqrt{x}\\ \Leftrightarrow6=6\sqrt{x}\\ \Leftrightarrow\sqrt{x}=1\\ \Leftrightarrow x=1\left(tm\right)\)