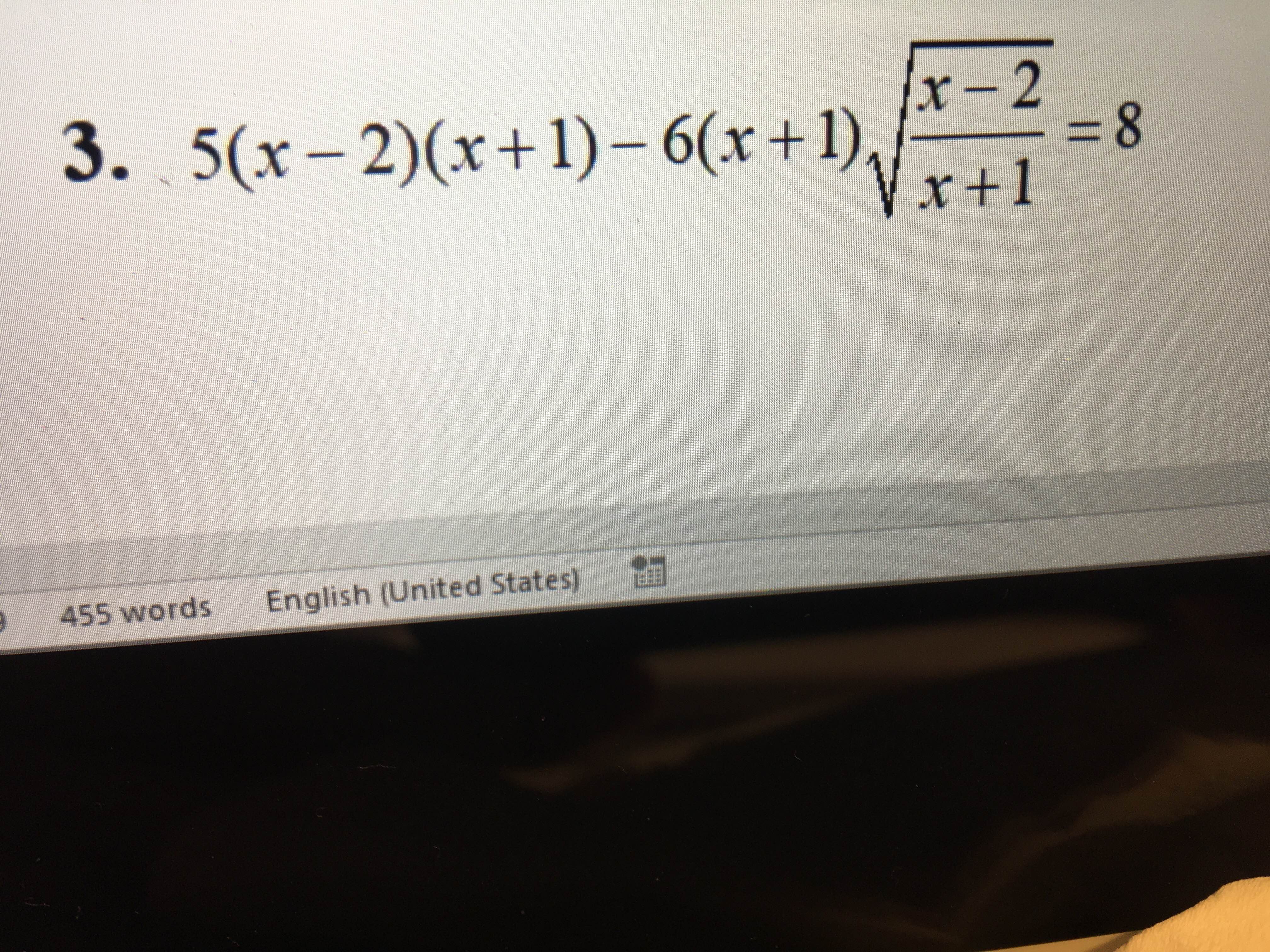ĐKXĐ\(x\ge2;x< -1\)
\(5\left(x-2\right)\left(x+1\right)-6\left(x+1\right)\sqrt{\dfrac{x-2}{x+1}}=8\\ \Leftrightarrow5\left(x-2\right)\left(x+1\right)-6\sqrt{\left(x-2\right)\left(x+1\right)}=8\left(1\right)\)
Đặt \(\sqrt{x-2}=a\ge0,\sqrt{x+1}=b\ge0\)
\(pt\left(1\right)\Leftrightarrow5a^2b^2-6ab=8\\ \Leftrightarrow5a^2b^2-6ab-8=0\\ \Leftrightarrow\left(5a^2b^2-10ab\right)+\left(4ab-8\right)=0\\ \Leftrightarrow5ab\left(ab-2\right)+4\left(ab-2\right)=0\\ \Leftrightarrow\left(ab-2\right)\left(5ab+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}ab=2\\5ab=-4\left(vô.lí\right)\end{matrix}\right.\\ \Leftrightarrow\sqrt{\left(x-2\right)\left(x+1\right)}=2\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=4\)
\(\Leftrightarrow x^2-x-2=4\\ \Leftrightarrow x^2-x-6=0\\ \Leftrightarrow\left(x-3\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-2\left(tm\right)\end{matrix}\right.\)
\(ĐK:x\ge2;x< -1\)
Đặt \(\left\{{}\begin{matrix}x+1=a\\x-2=b\end{matrix}\right.,PTTT:\)
\(5ab-6a\cdot\sqrt{\dfrac{b}{a}}=8\\ \Leftrightarrow5ab-6\sqrt{ab}-8=0\\ \Leftrightarrow\left(\sqrt{ab}-2\right)\left(5\sqrt{ab}+4\right)=0\\ \Leftrightarrow\sqrt{ab}=2\left(5\sqrt{ab}+4>0\right)\\ \Leftrightarrow ab=4\\ \Leftrightarrow\left(x-2\right)\left(x+1\right)=4\\ \Leftrightarrow x^2-x-6=0\\ \Leftrightarrow\left(x-3\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-2\left(tm\right)\end{matrix}\right.\)