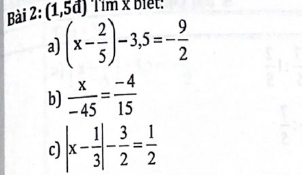Question

Answer 1

môn toán mà =))

Answer 2

c) \(\left|x-\dfrac{1}{3}\right|-\dfrac{3}{2}=\dfrac{1}{2}\Rightarrow\left|x-\dfrac{1}{3}\right|=\dfrac{1}{2}+\dfrac{3}{2}\Rightarrow\left|x-\dfrac{1}{3}\right|=2\Rightarrow x-\dfrac{1}{3}=2\text{hoặc}=-2\)TH1:  \(x-\dfrac{1}{3}=2\\ x=2+\dfrac{1}{3}=\dfrac{6+1}{3}=\dfrac{7}{3}\)

TH2: \(x-\dfrac{1}{3}=-2\\ x=-2+\dfrac{1}{3}=\dfrac{-6+1}{3}=\dfrac{-5}{3}\)

Vậy \(x=\left\{\dfrac{7}{3};\dfrac{-5}{3}\right\}\)

Answer 3

b) \(\dfrac{x}{-45}=\dfrac{-4}{15}\Rightarrow x.15=\left(-4\right).\left(-45\right)\\ x.15=180\\ x=180:15=12\)

Answer 4

a) \(\left(x-\dfrac{2}{5}\right)-3,5=-\dfrac{9}{2}\\ x-\dfrac{2}{5}=-4,5+3,5\\ x-0,4=-1\\ x=-1+0,4=-0,6\)