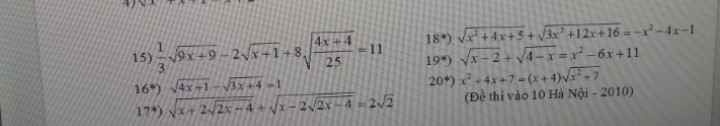\(20,x^2+4x+7=\left(x+4\right)\sqrt{x^2+7}\\ \Leftrightarrow x^2-9=\left(x+4\right)\sqrt{x^2+7}-4\left(x+4\right)\\ \Leftrightarrow x^2-9=\left(x+4\right)\left[\sqrt{x^2+7}-4\right]\\ \Leftrightarrow x^2-9=\dfrac{\left(x+4\right)\left(x^2-9\right)}{\sqrt{x^2+7}+4}\\ \Leftrightarrow\left(x^2-9\right)\left(\dfrac{x+4}{\sqrt{x^2+7}+4}-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\\\dfrac{x+4}{\sqrt{x^2+7}+4}=1\left(1\right)\end{matrix}\right.\\ \left(1\right)\Leftrightarrow x+4=\sqrt{x^2+7}+4\\ \Leftrightarrow x=\sqrt{x^2+7}\Leftrightarrow x^2=x^2+7\Leftrightarrow0x^2=7\left(vô.n_o\right)\)
Do đó PT có 2 nghiệm là \(x=\pm3\)
\(19,ĐK:2\le x\le4\\ PT\Leftrightarrow\left(\sqrt{x-2}-1\right)-\sqrt{4-x}\left(\sqrt{4-x}-1\right)=x^2-5x+6\\ \Leftrightarrow\dfrac{x-3}{\sqrt{x-2}+1}-\dfrac{\sqrt{4-x}\left(3-x\right)}{\sqrt{4-x}+1}=\left(x-2\right)\left(x-3\right)\\ \Leftrightarrow\left(x-3\right)\left(\dfrac{1}{\sqrt{x-2}+1}+\dfrac{\sqrt{4-x}}{\sqrt{4-x}+1}+2-x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\\dfrac{1}{\sqrt{x-2}+1}+\dfrac{\sqrt{4-x}}{\sqrt{4-x}+1}+2-x=0\left(1\right)\end{matrix}\right.\)
Với \(2\le x\le4\Leftrightarrow\left(1\right)\) vô nghiệm
Vậy pt có nghiệm duy nhất \(x=3\)