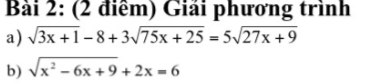a)ĐKXĐ: \(x\ge-\dfrac{1}{3}\)
\(\sqrt{3x+1}-8+3\sqrt{75x+25}=5\sqrt{27x+9}\\ \Rightarrow\sqrt{3x+1}-8+15\sqrt{3x+1}=15\sqrt{3x+1}\\ \Rightarrow\sqrt{3x+1}=8\\ \Rightarrow3x+1=64\\ \Rightarrow x=21\)
b) \(\sqrt{x^2-6x+9}+2x=6\\ \Rightarrow\sqrt{\left(x-3\right)^2}=6-2x\\ \Rightarrow\left|x-3\right|=6-2x\\ \Rightarrow\left[{}\begin{matrix}x-3=6-2x\\x-3=2x-6\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\x=3\end{matrix}\right.\\ \Rightarrow x=3\)
a) ĐKXĐ: \(x\ge-\dfrac{1}{3}\)
\(pt\Leftrightarrow\sqrt{3x+1}-8+15\sqrt{3x+1}=15\sqrt{3x+1}\)
\(\Leftrightarrow\sqrt{3x+1}=8\Leftrightarrow3x+1=64\)
\(\Leftrightarrow3x=63\Leftrightarrow x=21\left(tm\right)\)
b) ĐKXĐ: \(x\le3\)
\(pt\Leftrightarrow\sqrt{\left(x-3\right)^2}=6-2x\)
\(\Leftrightarrow\left|x-3\right|=6-2x\)
\(\Leftrightarrow x-3=2x-6\)(do \(x\le3\))
\(\Leftrightarrow x=3\left(tm\right)\)
a,
\(\sqrt{3x+1}-8+3\sqrt{75x+25}=5\sqrt{27x+9}\) ĐK:\(x\ge\dfrac{-1}{3}\)
đặt \(\sqrt{3x+1}=t\)
ta có t-8+15t=15t
===> \(t=64\)
===>x=21
b\(\sqrt{x^2-6x+9}+2x=6\)
\(\Leftrightarrow\left|x-3\right|=6-2x\)===>x=3