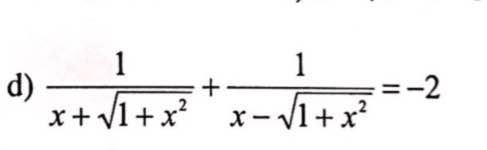\(\dfrac{1}{x+\sqrt{1+x^2}}+\dfrac{1}{x-\sqrt{1+x^2}}=-2\\ \Rightarrow\dfrac{x-\sqrt{1+x^2}}{\left(x+\sqrt{1+x^2}\right)\left(x-\sqrt{1+x^2}\right)}+\dfrac{x+\sqrt{1+x^2}}{\left(x+\sqrt{1+x^2}\right)\left(x-\sqrt{1+x^2}\right)}=-2\\ \)
\(\Rightarrow\dfrac{x-\sqrt{1+x^2}+x+\sqrt{1+x^2}}{\left(x+\sqrt{1+x^2}\right)\left(x-\sqrt{1+x^2}\right)}=-2\\ \Rightarrow\dfrac{2x}{x^2-1-x^2}=-2\\ \Rightarrow\dfrac{2x}{-1}=-2\\ \Rightarrow2x=2\\ \Rightarrow x=1\)
\(\dfrac{1}{x+\sqrt{1+x^2}}+\dfrac{1}{x-\sqrt{1+x^2}}=-2\left(đk:x\ge0\right)\)
\(\Leftrightarrow\dfrac{x-\sqrt{1+x^2}+x+\sqrt{1+x^2}}{\left(x+\sqrt{1+x^2}\right)\left(x-\sqrt{1+x^2}\right)}=-2\)
\(\Leftrightarrow\dfrac{2x}{x^2-1-x^2}=-2\Leftrightarrow-2x=-2\Leftrightarrow x=1\)
ĐK: \(x\in R\)
\(\dfrac{1}{x+\sqrt{1+x^2}}+\dfrac{1}{x-\sqrt{1+x^2}}=-2\)
\(\Leftrightarrow\dfrac{x-\sqrt{1+x^2}}{\left(x+\sqrt{1+x^2}\right)\left(x-\sqrt{1+x^2}\right)}+\dfrac{x+\sqrt{1+x^2}}{\left(x+\sqrt{1+x^2}\right)\left(x-\sqrt{1+x^2}\right)}=-2\)
\(\Leftrightarrow-2x=-2\)
\(\Leftrightarrow x=1\)