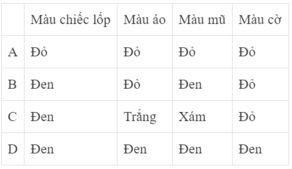
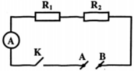
Cái này mình có hơi băn khoan một chút là các AMpe kế có ly tưởng hay không, mình đoán là có nên mình sẽ giải theo cách đó nhé
Ta có mạch điện mới tương đương với mạch đã cho
\(R_{CD}=\dfrac{4.4}{4+4}=2\left(\Omega\right)\)
\(R_{BD}=\dfrac{\left(2+2\right).4}{4+4}=2\left(\Omega\right)\)
\(R_{AD}=\dfrac{\left(2+2\right).4}{4+4}=2\left(\Omega\right)\)
\(U_{AD}=1.2=2\left(V\right)\)
\(I_3=\dfrac{U_{AD}}{R}=\dfrac{2}{4}=0,5\left(A\right)\Leftrightarrow\) Ampe kế 1 chỉ 0,5 A
\(I_{r1}=1-0,5=0,5\left(A\right)\)
\(U_{r1}=I_{r1}.r=0,5.2=1\left(V\right)\)
\(U_{BD}=2-1=1\left(V\right)\)
\(I_4=\dfrac{U_{BD}}{R}=\dfrac{1}{4}=0,25\left(A\right)\Leftrightarrow\) \(I_{A2}=I_4+I_3=0,25+0,5=0,75\left(A\right)\)
Vậy, Ampe kế 2 chỉ 0,75 A
\(I_{r2}=0,5-0,25=0,25\left(A\right)\)
\(U_{r2}=0,25.2=0,5\left(V\right)\)
\(U_{CD}=1-0,5=0,5\left(V\right)\)
\(I_6=\dfrac{0,5}{4}=0,125\left(A\right)\Leftrightarrow I_{A3}=I_m-I_6=1-0,125=0,875\left(A\right)\)
Vậy Ampe kế 3 chỉ 0,875 A