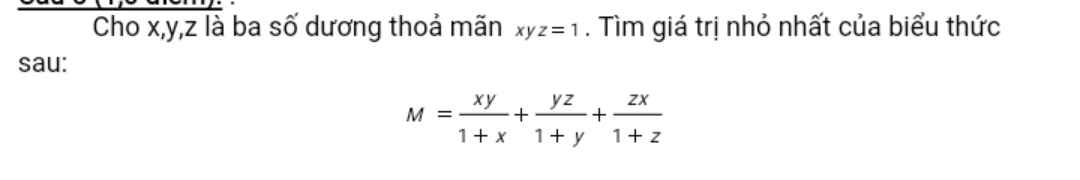Đặt \(\left(x,y,z\right)=\left(\dfrac{b}{a};\dfrac{c}{b};\dfrac{a}{c}\right)\).
Khi đó \(\dfrac{xy}{1+x}=\dfrac{\dfrac{b}{a}.\dfrac{c}{b}}{\dfrac{b}{a}+1}=\dfrac{c}{b+a}\). Tương tự,...
Ta có \(M=\dfrac{c}{b+a}+\dfrac{a}{c+b}+\dfrac{b}{a+c}\)
\(\Rightarrow M+3=\left(a+b+c\right)\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{c+a}\right)\ge\left(a+b+c\right).\dfrac{9}{a+b+b+c+c+a}=\dfrac{9}{2}\Rightarrow M\ge\dfrac{3}{2}\).
Đúng 1
Bình luận (2)
