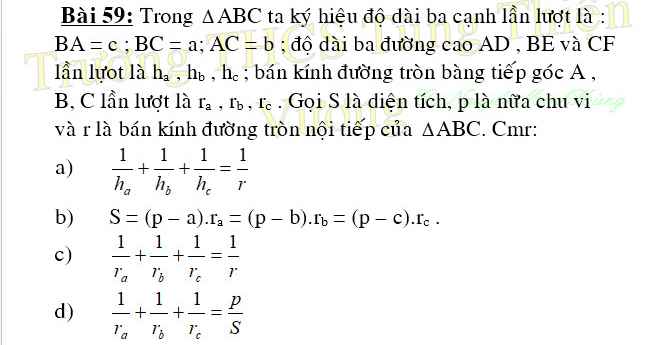a) Ta có công thức \(r=\dfrac{S}{p}\).
Từ đó \(\dfrac{1}{h_a}+\dfrac{1}{h_b}+\dfrac{1}{h_c}=\dfrac{1}{2S:a}+\dfrac{1}{2S:b}+\dfrac{1}{2S:c}=\dfrac{a}{2S}+\dfrac{b}{2S}+\dfrac{c}{2S}=\dfrac{2p}{2S}=\dfrac{p}{S}=\dfrac{1}{r}\).
b) Gọi tâm đường tròn bàng tiếp góc A của tam giác ABC là J, M, N, P lần lượt là tiếp điểm của (J) trên BC, CA, AB.
Khi đó JM = JN = JP = \(r_a\).
Ta có \(S_{ABC}=S_{JAB}+S_{JAC}-S_{JBC}=\dfrac{JP.AB}{2}+\dfrac{JP.AC}{2}-\dfrac{JP.BC}{2}=\dfrac{JP\left(AB+AC+BC-2BC\right)}{2}=\dfrac{JP\left(2p-2a\right)}{2}=r_a\left(p-a\right)\).
Tương tự ta có \(S=\left(p-a\right)r_a=\left(p-b\right)r_b=\left(p-c\right)r_c\).
c) Ta có \(\dfrac{1}{r_a}+\dfrac{1}{r_b}+\dfrac{1}{r_c}=\dfrac{p-a}{S}+\dfrac{p-b}{S}+\dfrac{p-c}{S}=\dfrac{3p-\left(a+b+c\right)}{S}=\dfrac{3p-2p}{S}=\dfrac{p}{S}=\dfrac{1}{r}\).
d) Giống câu c