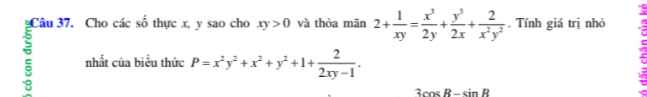Question

Answer 1

Áp dụng AM-GM

\(2+\dfrac{1}{xy}\ge2\sqrt{\dfrac{x^3}{2y}.\dfrac{y^3}{2x}}+\dfrac{2}{x^2y^2}=xy+\dfrac{2}{\left(xy\right)^2}\)

\(\rightarrow\)\(2+\dfrac{1}{xy}-xy-\dfrac{2}{\left(xy\right)^2}\ge0\)\(\rightarrow1\le xy\le2\)

\(P\ge2\sqrt{x^2y^2.1}+2\sqrt{x^2.y^2}+\dfrac{2}{2xy-1}=4xy+\dfrac{2}{2xy-1}=2\left(2xy-1\right)+\dfrac{2}{2xy-1}+2\ge2\sqrt{2\left(2xy-1\right).\dfrac{2}{2xy-1}}+2=6\)

Dấu "=" \(x=y=1\)

Answer 2

sử dụng cô si thuần là được

Do xy > 0 nên x,y cùng dấu do đó mấy phân số đó dương dẫn đến ...

Answer 3

mình dí nhầm chờ mình cập nhật nha