Cho hai đa thức :
\(P\left(x\right)=-5x^3-\dfrac{1}{3}+8x^4+x^2\)
\(Q\left(x\right)=x^2-5x-2x^3+x^4-\dfrac{2}{3}\)
Hãy tính \(P\left(x\right)+Q\left(x\right)\) và \(P\left(x\right)-Q\left(x\right)\) ?
Cho đa thức :
\(P\left(x\right)=x^4-3x^2+\dfrac{1}{2}-x\)
Tìm các đa thức \(Q\left(x\right),P\left(x\right)\) sao cho :
a) \(P\left(x\right)+Q\left(x\right)=x^5-2x^2+1\)
b) \(P\left(x\right)-R\left(x\right)=x^3\)
Ta có: P(x) = x4 - 3x2 + 1212 – x.
a) Vì P(x) + Q(x) = x5 – 2x2 + 1 nên
Q(x) = x5 – 2x2 + 1 - P(x)
Q(x) = x5 – 2x2 + 1 - x4 + 3x2 - 1212 + x
Q(x) = x5 - x4 + x2 + x + 1212
b) Vì P(x) - R(x) = x3 nên
R(x) = x4 - 3x2 + 1212 – x - x3
hay R(x) = x4 - x3 - 3x2 – x + 1212.
Viết đa thức \(P\left(x\right)=5x^3-4x^2+7x-2\) dưới dạng :
a) Tổng của hai đa thức một biến
b) Hiệu của hai đa thức một biến
Bạn Vinh nêu nhận xét : " Ta có thể viết đa thức đã cho thành tổng của hai đa thức bậc 4". Đúng hay sai ? Vì sao ?
Viết đa thức P(x) = 5x3 – 4x2 + 7x - 2 dưới dạng:
a) Tổng của hai đa thức một biến.
5x3 – 4x2 + 7x - 2 = (5x3 – 4x2) + (7x - 2)
b) Hiệu của hai đa thức một biến.
5x3 – 4x2 + 7x - 2 = (5x3 + 7x) - (4x2 + 2)
Chú ý: Đáp số ở câu a; b không duy nhất, các bạn có thể tìm thêm đa thúc khác.
Bạn Vinh nói đúng: Ta có thể viết đa thức đã cho thành tổng của hai đa thúc bậc 4 chẳng hạn như:
5x3 – 4x2 + 7x - 2 = (2x4 + 5x3 + 7x) + (– 2x4 – 4x2 - 2).
Cho các đa thức :
\(P\left(x\right)=2x^4-x-2x^3+1\)
\(Q\left(x\right)=5x^2-x^3+4x\)
\(H\left(x\right)=-2x^4+x^2+5\)
Tính \(P\left(x\right)+Q\left(x\right)+H\left(x\right)\) và \(P\left(x\right)-Q\left(x\right)-H\left(x\right)\) ?
Ta có:
P(x) = 2x4 –x - 2x3 + 1
Q(x) = 5x2 – x3 + 4x
H(x) = -2x4 + x2 + 5.
Sắp xếp các đa thức theo lũy thừa giảm dần rồi xếp các số hạng đồng dạng theo cùng cột dọc ta được:
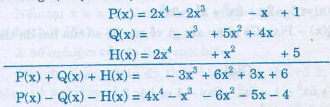
Chọn đa thức mà em cho là kết quả đúng :
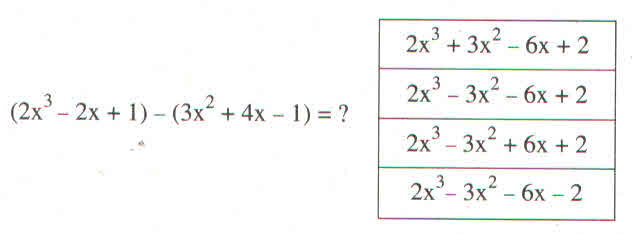
(2x3 - 2x + 1) - (3x2 + 4x - 1) = 2x3 - 3x2 - 6x + 2.
Vậy chọn đa thức thứ hai.
Hãy tìm bậc của mỗi đa thức sau :
\(M=x^2-2xy+5x^2-1\)
\(N=x^2y^2-y^2+5x^2-3x^2y+5\)
a) Đa thức M = x2 - 2xy + 5x2 - 1 = 6x2 - 2xy - 1 có bậc 2.
Đa thức N = x2y2 - y2 + 5x2 - 3x2y + 5 có bậc 4.
b) N + M = x2y2 – y2 + 11x2 – 3x2y + 4 – 2xy
N – M = x2y2 – y2 – x2 – 3x2y + 2xy + 6.
Cho các đa thức :
\(N=15y^3+5y^2-y^5-4y^3-2y\)
\(M=y^2+y^3-3y+1-y^2+y^5-y^3+7y^5\)
a) Thu gọn các đa thức trên
b) Tính N + M và N - M
a) Thu gọn các đa thức:
N = 15y3 + 5y2 - y5 - 5y2 - 4y3 - 2y = -y5 + 11y3 - 2y
M = y2 + y3 -3y + 1 - y2 + y5 - y3 + 7y5 = 8y5 - 3y + 1.
b) N + M = -y5 + 11y3 - 2y + 8y5 - 3y + 1
= 7y5 + 11y3 - 5y + 1
N - M = -y5 + 11y3 - 2y - 8y5 + 3y - 1= -9y5 + 11y3 + y - 1.
Cho hai đa thức :
\(P\left(x\right)=3x^2-5+x^4-3x^3-x^6-2x^2-x^3\)
\(Q\left(x\right)=x^3+2x^5-x^4+x^2-2x^3+x-1\)
a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến
b) Tính \(P\left(x\right)+Q\left(x\right)\) và \(P\left(x\right)-Q\left(x\right)\) ?
a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
Thu gọn: P(x) = 3x2 - 5 + x4 - 3x3 - x6 - 2x2 - x3
= x2 - 5 + x4 - 4x3 - x6
Sắp xếp: P(x) = -5 + x2 - 4x3 + x4 - x6
Thu gọn: Q(x) = x3 + 2x5 - x4 + x2 - 2x3 + x - 1= -x3 +2x5 - x4 + x2 + x - 1
Sắp xếp: Q(x) = -1 + x + x2 - x3 - x4 + 2x5
b) Ta có:
.
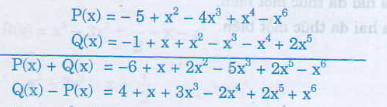Cho các đa thức :
\(P\left(x\right)=x^5-2x^4+x^2-x+1\)
\(Q\left(x\right)=6-2x+3x^3+x^4-3x^5\)
Tính \(P\left(x\right)-Q\left(x\right)\) và \(Q\left(x\right)-P\left(x\right)\) ?
Có nhận xét gì về các hệ số của hai đa thức tìm được ?
P (x) = x5 + 2x4 + x2 - x +1
Q (x) = 6 - 2x + 3x3 + x4 - 3x5
P (x) - Q (x) = (x5 + 2x4 + x2 - x +1) - ( 6 - 2x + 3x3 + x4 - 3x5)
= x5 + 2x4 + x2 - x +1 - 6 + 2x - 3x3 - x4 + 3x5
= ( x5 + 3x5 ) + ( 2x4 - x4 ) - 3x3 + x2 + ( -x + 2x ) +( 1 - 6 )
= 4x5 + x4 - 3x3 + x2 + x - 5
Q (x) - P (x) = ( 6 - 2x + 3x3 + x4 - 3x5 ) - (x5 + 2x4 + x2 - x +1)
= 6 - 2x + 3x3 + x4 - 3x5 - x5 - 2x4 - x2 + x -1
= - ( 3x5 + x5 ) + ( x4 - 2x4 ) + 3x3 - x2 - ( 2x - x ) + ( 6 - 1)
= - 4x5 - x4 + 3x3 - x2 - x + 5
* Nhận xét: Hệ số của hai đa thức P (x) và Q(x) đối nhau.
Trả lời bởi Dao DaoCho các đa thức :
\(P\left(x\right)=x^5-2x^4+x^2-x+1\)
\(Q\left(x\right)=6-2x+3x^3+x^4-3x^5\)
Tính \(P\left(x\right)-Q\left(x\right)\) và \(Q\left(x\right)-P\left(x\right)\) ?
Có nhận xét gì về các hệ số của hai đa thức tìm được ?
Ta có: P(x) = -5x3 - 1313 + 8x4 + x2 và Q(x) = x2 – 5x – 2x3 + x4 - 2323.
Ta sắp xếp hai đa thức theo lũy thừa giảm dần của biến như sau:
Trả lời bởi Quang Duy