Cho hàm số bậc nhất \(y=ax+3\)
a) Xác định hệ số góc a, biết rằng đồ thị của hàm số điqua điểm \(A\left(2;6\right)\)
b) Vẽ đồ thị của hàm số
Cho hàm số bậc nhất \(y=ax+3\)
a) Xác định hệ số góc a, biết rằng đồ thị của hàm số điqua điểm \(A\left(2;6\right)\)
b) Vẽ đồ thị của hàm số
Cho hàm số \(y=-2x+3\)
a) Vẽ đồ thị của hàm số
b) Tính góc tạo bởi đường thẳng \(y=-2x+3\) và trục Ox (làm tròn đến phút)
a) Đồ thị được vẽ như hình bên.
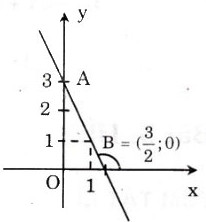
b) Gọi α là góc giữa đường thẳng y = -2x + 3 và trục Ox.
Thế thì 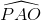 = 1800 - α.
= 1800 - α.
Ta có tg 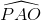 =
= 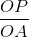 =
= 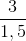 = 2.
= 2.
Suy ra 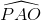 ≈ 63026’
≈ 63026’
Vậy α ≈ 116034’.
Trả lời bởi Nguyễn Đinh Huyền MaiXác định hàm số bậc nhất \(y=ax+b\) trong mỗi trường hợp sau :
a) a = 2 và đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng 1,5
b) a = 3 và đồ thị của hàm số đi qua điểm A( 2; 2)
c) Đồ thị của hàm số song song với đường thẳng \(y=\sqrt{3}x\) và đi qua điểm \(B\left(1;\sqrt{3}+5\right)\)
a) Hàm số đã cho là y = 2x + b.
Vì đồ thị đi qua điểm A(1,5; 0) nên 0 = 2 . 1,5 + b. Suy ra b = -3.
Vậy hàm số đã cho là y = 2x - 3.
b) Hàm số đã cho là y = 3x + b.
Vì đồ thị đi qua điểm A(2; 2) nên 2 = 3 . 2 + b. Suy ra b = -4.
Vậy hàm số đã cho là y = 3x - 4.
c) Vì đồ thị của hàm số đã cho song song với đường thẳng y = √3x nên nó có hệ số góc là a = √3. Do đó hàm số đã cho là y = √3x + b.
Vì đồ thị đi qua điểm B(1; √3 + 5) nên √3 + 5 = √3 . 1 + b. Suy ra b = 5.
Vậy hàm số đã cho là y = √3x + 5.
Trả lời bởi Nguyễn Đinh Huyền Maia) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số sau :
\(y=\dfrac{1}{2}x+2\) \(y=-x+2\)
b) Gọi giao điểm của hai đường thẳng \(y=\dfrac{1}{2}x+2\) ;\(y=-x+2\) với trục hoành theo thứ tự là A, B và gọi giao điểm của hai đường thẳng đó là C. Tính các góc của tam giác ABC (làm tròn đến độ)
c) Tính chu vi và diện tích của tam giác ABC (đơn vị đo trên các trục tọa độ là cm)
a) Đồ thị được vẽ như hình bên.
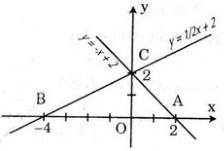
b) Giao của đường thẳng y = -x + 2 với Ox là B(2; 0).
Vì hai đường thẳng y = 0,5x + 2 và y = -x + 2 đều có tung độ gốc là 2 nên giao của chúng là C(0; 2).
Ta có tg A = 0,5. Suy ra 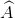 ≈ 26034’.
≈ 26034’.
Vì ∆BOC là tam giác vuông cân nên 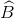 =450 .
=450 .
Suy ra 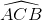 ≈ 1800 – (26034’ + 450) = 108026’.
≈ 1800 – (26034’ + 450) = 108026’.
c) Ta có AB = 6 (cm), AC = 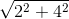 = 2√5 (cm), BC = 2√2 (cm).
= 2√5 (cm), BC = 2√2 (cm).
Do đó chu vi của ∆ABC là 6 + 2√5 + 2√2 (cm).
Diện tích của ∆ABC là:  AB . OC =
AB . OC =  . 6 . 2 = 6 (cm2).
. 6 . 2 = 6 (cm2).
a) Vẽ đồ thị của các hàm số \(y=x+1;y=\dfrac{1}{\sqrt{3}}x+\sqrt{3};y=\sqrt{3}x-\sqrt{3}\)
b) Gọi \(\alpha,\beta,\gamma\) lần lượt là các góc tạo bởi các đường thẳng trên và trục Ox
Chứng minh rằng :
\(tg\alpha=1;tg\beta=\dfrac{1}{\sqrt{3}};tg\gamma=\sqrt{3}\)
Tính số đo góc \(\alpha,\beta,\gamma\)
a) Đồ thị như hình bên.
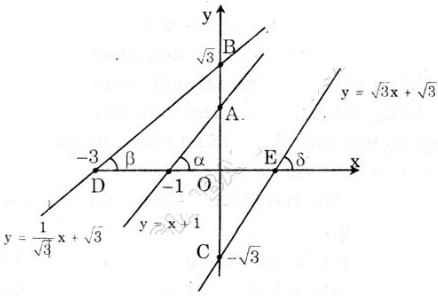
b) tgα = 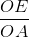 = 1,
= 1,
tgβ = 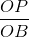 =
= 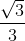 =
= 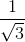 ,
,
tgɣ = 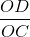 =
= 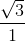 = √3.
= √3.
Suy ra α = 450, β = 300, ɣ = 600 .
Trả lời bởi Nguyễn Đinh Huyền Maia) Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm A(2; 1)
b) Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm B( 1; -2)
c) Vẽ đồ thị của các hàm số với hệ số góc tìm được ở các câu a), b) trên cùng một mặt phẳng tọa độ và chứng tỏ rằng hai đường thẳng đó vuông góc với nhau
Cho hai đường thẳng :
\(y=ax+b\) (d)
\(y=a'x+b\) (d')
Chứng minh rằng :
Trên cùng một mặt phẳng tọa độ, hai đường thẳng (d) và (d') vuông góc với nhau khi và chỉ khi \(a.a'=-1\)
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số sau :
\(y=x\) (1)
\(y=0,5x\) (2)
b) Đường thẳng (d) song song với trục Ox và cắt trục tung Oy tại điểm C có tung độ bằng 2, theo thứ tự cắt các đường thẳng (1) và (2) tại D và E. Tìm tọa độ của các điểm D, E. Tính chu vi và diện tích của tam giác ODE ?
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số :
\(y=-2x\) (1)
\(y=0,5x\) (2)
b) Qua điểm K(0; 2) vẽ đường thẳng (d) song song với trục Ox. Đường thẳng (d) cắt các đường thẳng (1), (2) lần lượt tại A và B. Tìm tọa độ của các điểm A, B
c) Hãy chứng tỏ rằng \(\widehat{AOB}=90^0\) (hai đường thẳng (1) và (2) vuông góc với nhau)

Từ đó ta có :
\(\widehat{AOK}=\widehat{OBK}\)
Mà \(\widehat{OBK}+\widehat{KOB}=90^0\) nên \(\widehat{AOK}+\widehat{KOB}=90^0\)
Trả lời bởi Nguyen Thuy HoaCho hàm số :
\(y=mx+\left(2m+1\right)\) (1)
Với mỗi giá trị của \(m\in\mathbb{R}\), ta có một đường thẳng xác định bởi (1). Như vậy, ta có một họ đường thẳng xác định bởi (1). Chứng minh rằng với mọi giá trị của m, họ đường thẳng xác định bởi (1) luôn đi qua một điểm cố định. Hãy xác định tọa độ của điểm đó ?
a) Vì đồ thi của hàm số đi qua điểm A(2; 6) nên ta có 6 = a.2 + 3.
Suy ra hệ số góc a = 3/2 và được hàm số y = 3/2x + 3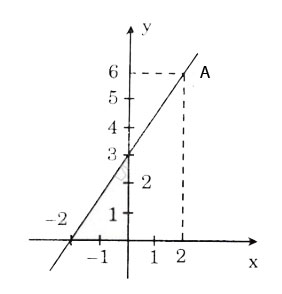
b) Hàm số đã cho là y = 3/2x + 3. Đồ thị được vẽ như hình bên.
Trả lời bởi Nguyễn Đinh Huyền Mai