Gieo một đồng tiền 3 lần
a) Mô tả không gian mẫu
b) Xác định các biến cố :
A: "Lần đầu xuất hiện mặt sấp"
B : " Mặt sất xảy ra đúng 1 lần"
C : "Mặt ngửa xảy ra ít nhất một lần"
Gieo một đồng tiền 3 lần
a) Mô tả không gian mẫu
b) Xác định các biến cố :
A: "Lần đầu xuất hiện mặt sấp"
B : " Mặt sất xảy ra đúng 1 lần"
C : "Mặt ngửa xảy ra ít nhất một lần"
Gieo một con súc sắc 2 lần :
a) Mô tả không gian mẫu
b) Phát biểu các biến cố sau dưới dạng mệnh đề
\(A=\left\{\left(6,1\right),\left(6,2\right),\left(6,3\right),\left(6,4\right),\left(6,5\right),\left(6,6\right)\right\}\)
\(B=\left\{\left(2,6\right),\left(6,2\right),\left(3,5\right),\left(5,3\right),\left(4,4\right)\right\}\)
\(C=\left\{\left(1,1\right),\left(2,2\right),\left(3,3\right),\left(4,4\right),\left(5,5\right),\left(6,6\right)\right\}\)
Phép thử T được xét là: "Gieo một con súc sắc hai lần".
a) Các phần tử của không gian mẫu của phép thử T được liệt kê trong bảng sau đây.
Trong bảng này, cột I là các mặt i chấm có thể xảy ra ở lần gieo thứ nhất, i = 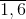 .
.
Dòng II (dòng trên cùng) là các mặt j chấm có thể xảy ra ở lần gieo thứ 2, j = 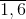 . Mỗi ô (i, j) (giao của dòng i và cột j, 1 ≤ i, j ≤ 6) biểu thị một kết quả có thể có của phép thử T là: lần gieo thứ nhất ra mặt i chấm, lần gieo thứ 2 ra mặt j chấm.
. Mỗi ô (i, j) (giao của dòng i và cột j, 1 ≤ i, j ≤ 6) biểu thị một kết quả có thể có của phép thử T là: lần gieo thứ nhất ra mặt i chấm, lần gieo thứ 2 ra mặt j chấm.
Không gian mẫu:
Ta có thể mô tả không gian mẫu dưới dạng như sau:
Ω = {(i, j)  i, j = 1, 2, 3, 4, 5, 6},
i, j = 1, 2, 3, 4, 5, 6},
ở đó (i, j) là kết quả: " Lần đầu xuất hiện mặt i chấm, lần sau xuất hiện mặt j chấm".
Không gian mẫu có 36 phần tử.
b) A = "Lần gieo đầu được mặt 6 chấm";
B = "Tổng số chấm trong hai lần gieo là 8";
C = "Kết quả ở hai lần gieo là như nhau".
Một hộp chứa bốn cái thẻ được đánh số 1, 2, 3, 4. Lấy ngẫu nhiên hai thẻ :
a) Mô tả không gian mẫu
b) Xác định các biến cố sau :
A: "tổng các số trên hai thẻ là số chẵn"
B : "Tích các số trên hai thẻ là số chẵn"
Phép thử T được xét là: "Từ hộp đã cho, lấy ngẫu nhiên hai thẻ".
a) Đồng nhất mỗi thẻ với chữ số ghi trên thẻ đó, ta có: Mỗi một kết quả có thể có các phép thử là một tổ hợp chập 2 của 4 chữ số 1, 2, 3, 4. Do đó, số phần tử của không gian mẫu là C24 = 6, và không gian mẫu gồm các phần tử sau:
Ω = {(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)}.
b) A = {(1, 3), (2, 4)}.
B = {(1, 2), (1, 4), (2, 3), (2, 4), (3, 4)} = Ω {(1, 3)}
Hai xạ thủ cùng bắn vào bia. Kí hiệu \(A_K\) là biến cố : "Người thứ k bắn trúng", k = 1, 2
a) Hãy biểu diễn các biến cố dau qua các biến cố \(A_1,A_2\)
A: "Không ai bắn trúng"
B : " Cả hai đều bắn trúng"
C: " Có đúng một người bắn trúng"
D : " Có ít nhất một người bắn trúng"
b) Chứng tỏ rằng : \(A=\overline{D}\); B và C xung khắc
Phép thử T được xét là: "Hai xạ thủ cùng bắn vào bia".
Theo đề ra ta có = "Người thứ k không bắn trúng", k = 1, 2. Từ đó ta có:
a) A = "Không ai bắn trúng" = "Người thứ nhất không bắn trúng và người thứ hai không bắn trúng". Suy ra A = .
.
Tương tự, ta có B = "Cả hai đều bắn trúng" = .
.
Xét C = "Có đúng một người bắn trúng", ta có C là hợp của hai biến cố sau:
"Người thứ nhất bắn trúng và người thứ hai bắn trượt" = A1 . .
"Người thứ nhất bắn trượt và người thứ hai bắn trúng" = . A2 .
Suy ra C = A1 . ∪
. A2 .
Tương tự, ta có D = A1 ∪ A2 .
b) Gọi là biến cố: " Cả hai người đều bắn trượt". Ta có
=
.
= A.
Hiển nhiên B ∩ C = Φ nên suy ra B và C xung khắc với nhau.
Từ một hộp chứa 10 cái thẻ, trong đó các thẻ đánh số 1, 2, 3, 4, 5 mầu đỏ, thẻ đánh số 6 mầu xanh và các thẻ đánh số 7, 8, 9, 10 mầu trắng. Lấy ngẫu nhiên một thẻ
a) Mô tả không gian mẫu
b) Kí hiệu A, B, C là các biến cố sau :
A: "Lấy được thẻ mầu đỏ"
B : "Lấy được thẻ mầu trắng"
C : " Lấy được thẻ ghi số chẵn"
Hãy biểu diễn các biến cố A, B, C bởi các tập con tương ứng của không gian mẫu ?
Phép thử T được xét là: "Từ hộp đã cho, lấy ngẫu nhiên một thẻ".
a) Không gian mẫu được mô tả bởi tập
Ω = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
b) A = {1, 2, 3, 4, 5};
B = {7, 8, 9, 10};
C = {2, 4, 6, 8, 10}.
Gieo một đồng tiền liên tiếp cho đến khi lần đầu xuất hiện mặt sau hoặc cả 4 lần ngửa thì dừng lại :
a) Mô tả không gian mẫu
b) Xác định các biến cố
A : "Số lần gieo không vượt quá ba"
B : " Số lần gieo là bốn"
a) Không gian mẫu của phép thử đã cho là:
Ω = {S, NS, NNS, NNNS, NNNN}.
b) A = {S, NS, NNS};
B = {NNNS, NNNN}.
Từ một hộp chứa năm quả cầu được đánh số 1, 2, 3, 4, 5, lấy ngẫu nhiên liên tiếp hai lần mỗi lần một quả và xếp theo thứ tự từ trái qua phải.
a) Mô tả không gian mẫu
b) Xác định các biến cố sau :
A : "Chữ số sau lớn hơn chữ số trước"
B : " Chữ số trước gấp đôi chữ số sau"
C : " Hai chữ số bằng nhau"
Phép thử T được xét là: "Từ hộp đã cho, lấy ngẫu nhiên liên tiếp hai lần mỗi lần một quả và xếp theo thứ tự từ trái qua phải".
a) Mỗi một kết quả có thể có của phép thử T là một chỉnh hợp chập 2 của 5 quả cầu đã được đánh số 1, 2, 3, 4, 5. Do đó số các kết quả có thể có của phép thử T là
A25 = 20, và không gian mẫu của phép thử T bao gồm các phần tử sau:
Ω = {(1, 2), (2, 1), (1, 3), (3, 1), (1, 4), (4, 1), (1, 5), (5, 1), (2, 3), (3, 2), (2, 4), (4, 2), (2, 5), (5, 2), (3, 4), (4, 3), (3, 5), (5, 3), (4, 5), (5, 4)},
trong đó (i, j) là kết quả: "Lần đầu lấy được quả cầu đánh số j (xếp bên phải)",
1 ≤ i, j ≤ 5.
b) A = {(1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5)};
B = {(2, 1), (4, 2)};
C = Φ.
Trả lời bởi Lê Thiên Anh
Gieo một đồng tiền ba lần và quan sát sự xuất hiện mặt sấp (S), mặt ngửa (N)
a) Xây dựng không gian mẫu
b) Xác định các biến cố
A : "Lần gieo đầu xuất hiện mặt sấp"
B : "Ba lần xuất hiện các mặt như nhau"
C : " Đúng hai lần xuất hiện mặt sấp"
D : " Ít nhất một lần xuất hiện mặt sấp"
Gieo một đồng tiền, sau đó gieo một con súc sắt. Quan sát sự xuất hiện mặt sấp (S), mặt ngửa (N) của đồng tiền và số chấm xuất hiện trên con súc sắc.
a) Xây dựng không gian mẫu
b) Xác định các biến cố sau :
A : " Đồng tiền xuất hiện mặt sấp và con súc sắc xuất hiện mặt chẵn chấm"
B : " Đồng tiền xuất hiện mặt ngửa và con súc sắc xuất hiện mặt lẻ chấm"
C : " Mặt 6 chấm xuất hiện"
Một con súc sắc được gieo 3 lần. Quan sát số chấm xuất hiện
a) Xây dựng không gian mẫu
b) Xác định các biến cố sau :
A : " Tổng số chấm trong 3 lần gieo là 6"
B : " Số chấm trong lần gieo thứ nhất bằng tổng các số chấm của lần gieo thứ hai và thứ ba"
Không gian (KG) mẫu: gồm 8 phần tử
Ω = {SSS, SSN, SNS, SNN, NSS, NSN, NNS, NNN}.
Trong đó SSS là kết quả "ba lần gieo đồng tiền xuất hiện mặt sấp"; NSS là kết quả "lần đầu đồng tiền xuất hiện mặt ngửa, lần thứ 2, lần thứ 3 xuất hiện mặt sấp"
b) A = {SSS, SSN, SNS, SNN},
B = {SNN, NSN, NNS},
C = {SSN, SNS, SNN, NSS, NSN, NNS, NNN} = Ω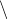 {SSS}.
{SSS}.
Trả lời bởi Lê Thiên Anh