Giải phương trình :
\(\sin^2x-\sin x=0\)
Giải phương trình :
\(\sin^2x-\sin x=0\)
Giải các phương trình sau :
a) \(2\cos^2x-3\cos x+1=0\)
b) \(2\sin2x+\sqrt{2}\sin4x=0\)
a) Đặt t = cosx, t ∈ [-1 ; 1] ta được phương trình 2t2 - 3t + 1 = 0 ⇔ t ∈ {1 ; ![]() }.
}.
Nghiệm của phương trình đã cho là các nghiệm của hai phương trình sau:
cosx = 1 ⇔ x = k2π và cosx = ![]() ⇔ x =
⇔ x = ![]() + k2π.
+ k2π.
Đáp số : x = k2π ; x = ![]() + k2π, k ∈ Z.
+ k2π, k ∈ Z.
b) Ta có sin4x = 2sin2xcos2x (công thức nhân đôi), do đó phương trình đã cho tương đương với
2sin2x(1 + √2cos2x) = 0 ⇔ ![]()
⇔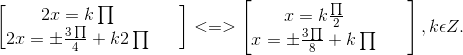
Giải các phương trình sau :
a) \(\sin^2\dfrac{x}{2}-2\cos\dfrac{x}{2}+2=0\)
b) \(8\cos^2x+2\sin x-7=0\)
c) \(2\tan^2c+3\tan x+1=0\)
d) \(\tan x-2\cos x+1=0\)
a) Đặt t = cos![]() , t ∈ [-1 ; 1] thì phương trình trở thành
, t ∈ [-1 ; 1] thì phương trình trở thành
(1 - t2) - 2t + 2 = 0 ⇔ t2 + 2t -3 = 0 ⇔ ![]()
Phương trình đã cho tương đương với
cos![]() = 1 ⇔
= 1 ⇔ ![]() = k2π ⇔ x = 4kπ, k ∈ Z.
= k2π ⇔ x = 4kπ, k ∈ Z.
b) Đặt t = sinx, t ∈ [-1 ; 1] thì phương trình trở thành
8(1 - t2) + 2t - 7 = 0 ⇔ 8t2 - 2t - 1 = 0 ⇔ t ∈ {![]() }.
}.
Các nghiệm của phương trình đã cho là nghiệm của hai phương trình sau :
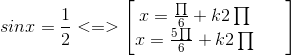
và ![]()
Đáp số : x = ![]() + k2π; x =
+ k2π; x = ![]() + k2π;
+ k2π;
x = arcsin(![]() ) + k2π; x = π - arcsin(
) + k2π; x = π - arcsin(![]() ) + k2π, k ∈ Z.
) + k2π, k ∈ Z.
c) Đặt t = tanx thì phương trình trở thành 2t2 + 3t + 1 = 0 ⇔ t ∈ {-1 ; ![]() }.
}.
Vậy ![]()
d) Đặt t = tanx thì phương trình trở thành
t - ![]() + 1 = 0 ⇔ t2 + t - 2 = 0 ⇔ t ∈ {1 ; -2}.
+ 1 = 0 ⇔ t2 + t - 2 = 0 ⇔ t ∈ {1 ; -2}.
Vậy ![]()
Giải các phương trình sau :
a) \(2\sin^2x+\sin x\cos x-3\cos^2x=0\)
b) \(3\sin^2-4\sin x\cos x+5\cos^2x=2\)
c) \(\sin^2x+\sin2x-2\cos^2+5\cos^2x=2\)
d) \(2\cos^2x-3\sqrt{3}\sin2x-4\sin^2x=-4\)
a) Dễ thấy cosx = 0 không thỏa mãn phương trình đã cho nên chiaw phương trình cho cos2x ta được phương trình tương đương 2tan2x + tanx - 3 = 0.
Đặt t = tanx thì phương trình này trở thành
2t2 + t - 3 = 0 ⇔ t ∈ {1 ; ![]() }.
}.
Vậy ![]()
b) Thay 2 = 2(sin2x + cos2x), phương trình đã cho trở thành
3sin2x - 4sinxcosx + 5cos2x = 2sin2x + 2cos2x
⇔ sin2x - 4sinxcosx + 3cos2x = 0
⇔ tan2x - 4tanx + 3 = 0
⇔ ![]()
⇔ x = ![]() + kπ ; x = arctan3 + kπ, k ∈ Z.
+ kπ ; x = arctan3 + kπ, k ∈ Z.
c) Thay sin2x = 2sinxcosx ; ![]() =
= ![]() (sin2x + cos2x) vào phương trình đã cho và rút gọn ta được phương trình tương đương
(sin2x + cos2x) vào phương trình đã cho và rút gọn ta được phương trình tương đương
![]() sin2x + 2sinxcosx -
sin2x + 2sinxcosx - ![]() cos2x = 0 ⇔ tan2x + 4tanx - 5 = 0 ⇔
cos2x = 0 ⇔ tan2x + 4tanx - 5 = 0 ⇔ ![]()
⇔ x = ![]() + kπ ; x = arctan(-5) + kπ, k ∈ Z.
+ kπ ; x = arctan(-5) + kπ, k ∈ Z.
d) 2cos2x - 3√3sin2x - 4sin2x = -4
⇔ 2cos2x - 3√3sin2x + 4 - 4sin2x = 0
⇔ 6cos2x - 6√3sinxcosx = 0 ⇔ cosx(cosx - √3sinx) = 0
⇔ 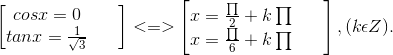
Giải các phương trình sau :
a) \(\cos x-\sqrt{3}\sin x=\sqrt{2}\)
b) \(3\sin3x-4\cos3x=5\)
c) \(2\sin x+2\cos x-\sqrt{2}=0\)
d) \(5\cos2x+12\sin2x-13=0\)
a) cosx - √3sinx = √2 ⇔ cosx - tan![]() sinx = √2
sinx = √2
⇔ cos![]() cosx - sin
cosx - sin![]() sinx = √2cos
sinx = √2cos![]() ⇔ cos(x +
⇔ cos(x + ![]() ) =
) = ![]()
⇔ 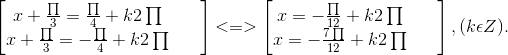
Trả lời bởi Phan Thùy Linh
Giải các phương trình sau :
a) \(\tan\left(2x+1\right)\tan\left(3x-1\right)=1\)
b) \(\tan x+\tan\left(x+\dfrac{\pi}{4}\right)=1\)
a) tan(2x + 1)tan(3x - 1) = 1 ⇔ = 1.
Với điều kiện cos(2x + 1)cos(3x - 1) ≠ 0 phương trình tương đương với
cos(2x + 1)cos(3x - 1) - sin(2x + 1)sin(3x - 1) = 0
⇔ cos(2x + 1 + 3x - 1) = 0 ⇔ 5x = + k π ⇔ x =
+
, k ∈ Z.
Cần chọn các k nguyên để x = +
không thỏa mãn điều kiện của phương trình (để loại bỏ). Điều này chỉ xảy ra trong các trường hợp sau:
(i) x = +
làm cho cos(2x + 1) = 0, tức là
cos[2( +
) + 1] = 0 ⇔
+ 1 =
+ lπ, (l ∈ Z)
⇔ π( -
) = 1 ⇔ π =
, suy ra π ∈ Q, vô lí.
Vì vậy không có k nguyên nào để x = +
làm cho cos(2x + 1) = 0.
(ii) x = +
làm cho cos(3x - 1) = 0. Tương tự (i),ta cũng thấy không có k nguyên nào để x =
+
làm cho cos(3x - 1) = 0.
Vậy ∀ k ∈ Z, x = +
đều là nghiệm của phương trình đã cho.
b)Đặt t = tan x, phương trình trở thành
t + = 1 ⇔ -t2 + 3t = 0 (điều kiện t ≠ 1) ⇔ t = 0 hoặc t = 3 (thỏa mãn)
Vậy tan x = 0 ⇔ x = kπ
tan x = 3 ⇔ x = arctan 3 + kπ (k ∈ Z)
Giải các phương trình sau :
a) \(\cos2x-\sin x-1=0\)
b) \(\cos x\cos2x=1+\sin x\sin2x\)
c) \(4\sin x\cos x\cos2x=-1\)
d) \(\tan x=3\cot x\)
Giải các phương trình sau :
a) \(\sin x+2\sin3x=-\sin5x\)
b) \(\cos5x\cos x=\cos4x\)
c) \(\sin x\sin2x\sin3x=\dfrac{1}{4}\sin4x\)
d) \(\sin^4x+\cos^4x=-\dfrac{1}{2}\cos^22x\)
Giải các phương trình sau :
a) \(3\cos^2x-2\sin x+2=0\)
b) \(5\sin^2x+3\cos x+3=0\)
c) \(\sin^6x+\cos^6x=4\cos^22x\)
d) \(-\dfrac{1}{4}+\sin^2x=\cos^4x\)
Giải các phương trình sau :
a) \(2\tan x-3\cot x-2=0\)
b) \(\cos^2=3\sin2x+3\)
c) \(\cot x-\cot2x=\tan x+1\)
sin2x - sinx = 0 ⇔ sinx(sinx - 1) = 0
Th1. sinx=0 \(\Leftrightarrow\) x=kπ \(\left(k\in Z\right)\)
Th2. sinx=1\(\Leftrightarrow\) x= \(\dfrac{\text{π}}{2}\) + \(\text{k 2 π}\)\(\left(k\in Z\right)\)
Vậy phương trình có hai họ nghiệm là:
- \(x=k\pi\) và \(x=\dfrac{\pi}{2}+k2\pi\) với \(\left(k\in Z\right)\)
Trả lời bởi Vương Khả Thiên Di