Bài 3. Đường tiệm cận của đồ thị hàm số

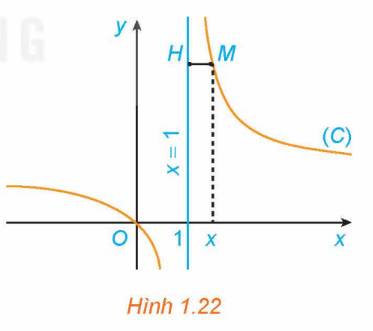
a) Ta có: \(M\left( {x;\frac{{2x + 1}}{x}} \right)\); \(H\left( {x;2} \right)\).

Do đó, \(MH = \sqrt {{{\left( {x - x} \right)}^2} + {{\left( {2 - \frac{{2x + 1}}{x}} \right)}^2}}  = \sqrt {{{\left( {\frac{{2x - 2x - 1}}{x}} \right)}^2}}  = \frac{1}{x}\) (do \(x > 0\))

b) Ta có: \(\mathop {\lim }\limits_{x \to  + \infty } \frac{1}{x} = 0\). Do đó, khi \(x \to  + \infty \) thì \(MH \to 0\).

Ta có: \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{2x - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to  + \infty } \frac{{2 - \frac{1}{x}}}{{1 - \frac{1}{x}}} = 2;\mathop {\lim }\limits_{x \to  - \infty } \frac{{2x - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to  - \infty } \frac{{2 - \frac{1}{x}}}{{1 - \frac{1}{x}}} = 2\).

Do đó, tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x - 1}}{{x - 1}}\) là \(y = 2\).

Ta có: \(\mathop {\lim }\limits_{t \to  + \infty } m\left( t \right) = \mathop {\lim }\limits_{t \to  + \infty } 15{e^{ - 0,012t}} = \mathop {\lim }\limits_{t \to  + \infty } \frac{{15}}{{{e^{0,012t}}}} = 0\)

Do đó, \(m\left( t \right) \to 0\) khi \(t \to  + \infty \).

Trong hình 1.18, khi \(t \to  + \infty \) thì m(t) càng gần trục hoành Ot (nhưng không chạm trục Ot).

a) Ta có: \(M\left( {x;\frac{x}{{x - 1}}} \right);H\left( {1;\frac{x}{{x - 1}}} \right)\)

Do đó, \(MH = \sqrt {{{\left( {1 - x} \right)}^2} + {{\left( {\frac{x}{{x - 1}} - \frac{x}{{x - 1}}} \right)}^2}}  = x - 1\) (do \(x > 1\))

b) Khi khoảng cách MH dần đến 0 thì tung độ của điểm M dần ra xa vô tận về phía trên (tung độ điểm M tiến ra \( + \infty \)).

Ta có: \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{2x + 1}}{{x - 4}} = \mathop {\lim }\limits_{x \to  + \infty } \frac{{2 + \frac{1}{x}}}{{1 - \frac{4}{x}}} = 2;\mathop {\lim }\limits_{x \to  - \infty } \frac{{2x + 1}}{{x - 4}} = \mathop {\lim }\limits_{x \to  - \infty } \frac{{2 + \frac{1}{x}}}{{1 - \frac{4}{x}}} = 2\) nên tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x + 1}}{{x - 4}}\) là \(y = 2\).

Lại có: \(\mathop {\lim }\limits_{x \to {4^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {4^ + }} \frac{{2x + 1}}{{x - 4}} =  + \infty ;\mathop {\lim }\limits_{x \to {4^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {4^ - }} \frac{{2x + 1}}{{x - 4}} =  - \infty \) nên tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x + 1}}{{x - 4}}\) đường thẳng \(x = 4\).

Ta có: \(\mathop {\lim }\limits_{p \to {{100}^ - }} C\left( p \right) = \mathop {\lim }\limits_{p \to {{100}^ - }} \frac{{45p}}{{100 - p}} =  + \infty \) nên tiệm cận đứng của đồ thị hàm số C(p) là \(p = 100\).

Ý nghĩa của đường tiệm cận là: Không thể loại bỏ hết loài tảo độc ra khỏi hồ nước dù chi phí là bao nhiêu.

a) Nhìn vào đồ thị ta thấy, khi \(x \to  + \infty \) thì khoảng cách MH tiến tới 0.

b) Ta có: \(\mathop {\lim }\limits_{x \to  + \infty } \left[ {f\left( x \right) - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to  + \infty } \left[ {x - 1 + \frac{2}{{x + 1}} - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to  + \infty } \frac{2}{{x + 1}} = \mathop {\lim }\limits_{x \to  + \infty } \frac{{\frac{2}{x}}}{{1 + \frac{1}{x}}} = 0\)

Tính chất này được thể hiện trong Hình 1.24 là: Khoảng cách từ điểm M của đồ thị hàm số (C) đến đường thẳng \(y = x - 1\) tiến đến 0 khi \(x \to  + \infty \).

Ta có: \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 4x + 2}}{{1 - x}} =  + \infty \); \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} - 4x + 2}}{{1 - x}} =  - \infty \)

Vậy tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\) là đường thẳng \(x = 1\)

Ta có: \(y = f\left( x \right) = \frac{{{x^2} - 4x + 2}}{{1 - x}} =  - x + 3 - \frac{1}{{1 - x}}\)

Do đó, \(\mathop {\lim }\limits_{x \to  + \infty } \left[ {f\left( x \right) - \left( { - x + 3} \right)} \right] = \mathop {\lim }\limits_{x \to  + \infty } \frac{{ - 1}}{{1 - x}} = 0\), \(\mathop {\lim }\limits_{x \to  - \infty } \left[ {f\left( x \right) - \left( { - x + 3} \right)} \right] = \mathop {\lim }\limits_{x \to  - \infty } \frac{{ - 1}}{{1 - x}} = 0\)

Vậy tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right)\) là đường thẳng \(y =  - x + 3\)

a) \(\mathop {\lim }\limits_{x \to  - \infty } f\left( x \right) = 2\); \(\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) = 2\); \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) =  - \infty \); \(\mathop {\lim }\limits_{x \to  - {1^ + }} f\left( x \right) =  - \infty \)

b) Do đó, tiệm cận đứng của đồ thị hàm số là \(x = 1;x =  - 1\).

Tiệm cận ngang của đồ thị hàm số là \(y = 2\)

Ta có: \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} + 2x - 3}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{\left( {x - 1} \right)\left( {x + 3} \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ + }} \left( {x + 3} \right) = 4\)

\(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} + 2x - 3}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{\left( {x - 1} \right)\left( {x + 3} \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ - }} \left( {x + 3} \right) = 4\)

Do đó, đường thẳng \(x = 1\) không là tiệm cận đứng của đồ thị hàm số \(y = \frac{{{x^2} + 2x - 3}}{{x - 1}}\).