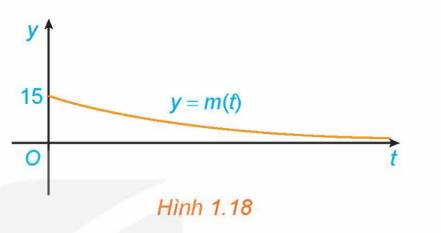
Ta có: \(\mathop {\lim }\limits_{t \to + \infty } m\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } 15{e^{ - 0,012t}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{15}}{{{e^{0,012t}}}} = 0\)
Do đó, \(m\left( t \right) \to 0\) khi \(t \to + \infty \).
Trong hình 1.18, khi \(t \to + \infty \) thì m(t) càng gần trục hoành Ot (nhưng không chạm trục Ot).
Đúng 0
Bình luận (0)