Hình 1.26 là đồ thị của hàm số \(y = f\left( x \right) = \frac{{2{x^2}}}{{{x^2} - 1}}\)
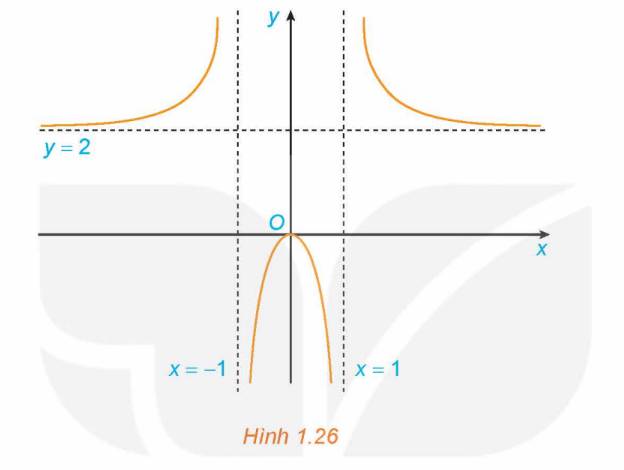
Sử dụng đồ thị này, hãy:
a) Viết kết quả của các giới hạn sau: \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)\); \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\); \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right)\); \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right)\)
b) Chỉ ra các tiệm cận của đồ thị hàm số đã cho.

a) \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2\); \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\); \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) = - \infty \)
b) Do đó, tiệm cận đứng của đồ thị hàm số là \(x = 1;x = - 1\).
Tiệm cận ngang của đồ thị hàm số là \(y = 2\)
Trả lời bởi Hà Quang Minh