Bài 3: Đường thẳng vuông góc với mặt phẳng
Các câu hỏi tương tự
Cho hình chóp S.ABCD có đáy là hình thoi ABCD và SA = SB = SC = SD. Gọi O là giao điểm của AC và BD. Chứng minh rằng :
a) Đường thẳng SO vuông góc với mặt phẳng (ABCD)
b) Đường thẳng AC vuông góc với mặt phẳng (SBD) và đường thẳng BD vuông góc với mặt phẳng (SAC)
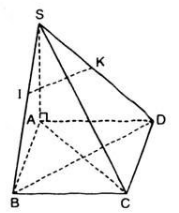
Cho hình chóp S.ABCD có đáy là hình vuông tâm O, AB SA a, SA vuông góc với (ABCD). Gọi (P) là mặt phẳng qua A và vuông góc với SC, (P) cắt SB, SC, SD lần lượt tại H, I, K.a, Chứng minh HK // BD.b, Chứng minh AH vuông góc với SB, AK vuông góc với SD.c, CM tứ giác AHIK có 2 đường chéo vuông góc. Tính diện tích AHIK theo a.Mình không xác định được mp (P) nên giúp mình vẽ cả hình nữa nhé! Cảm ơn nhiều.
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông tâm O, AB = SA = a, SA vuông góc với (ABCD). Gọi (P) là mặt phẳng qua A và vuông góc với SC, (P) cắt SB, SC, SD lần lượt tại H, I, K.
a, Chứng minh HK // BD.
b, Chứng minh AH vuông góc với SB, AK vuông góc với SD.
c, CM tứ giác AHIK có 2 đường chéo vuông góc. Tính diện tích AHIK theo a.
Mình không xác định được mp (P) nên giúp mình vẽ cả hình nữa nhé! Cảm ơn nhiều.
Cho hình chóp tứ giác $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$ và $SA$ vuông góc với mặt phẳng $(ABCD)$. Gọi $O$ là trung điểm của cạnh $SC$, $M$, $N$ lần lượt là trung điểm của các cạnh $SB$, $SD$. Gọi $P$ là điểm nằm trên đường thẳng $AN$ sao cho $OP perp AM$. Chứng minh rằng: $$frac{PM}{PN} frac{1}{3}.$$ **Lời giải:** Áp dụng định lí Menelaus lần lượt trên tam giác $ABC$ và $ACD$, ta có: $$frac{SM}{SB}cdot frac{BO}{OC}cdot frac{CQ}{QA} 1,$$ $$frac{SD}{SC}cdot frac{CO}{OB}cdot frac{BP}{...
Đọc tiếp
Cho hình chóp tứ giác $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$ và $SA$ vuông góc với mặt phẳng $(ABCD)$. Gọi $O$ là trung điểm của cạnh $SC$, $M$, $N$ lần lượt là trung điểm của các cạnh $SB$, $SD$. Gọi $P$ là điểm nằm trên đường thẳng $AN$ sao cho $OP \perp AM$. Chứng minh rằng: $$\frac{PM}{PN} = \frac{1}{3}.$$ **Lời giải:** Áp dụng định lí Menelaus lần lượt trên tam giác $ABC$ và $ACD$, ta có: $$\frac{SM}{SB}\cdot \frac{BO}{OC}\cdot \frac{CQ}{QA} = 1,$$ $$\frac{SD}{SC}\cdot \frac{CO}{OB}\cdot \frac{BP}{PA} = 1,$$ trong đó $Q$ là giao điểm của $SN$ và $OM$. Do đó, ta có: $$\frac{SM}{SB} = \frac{SC}{SO},$$ $$\frac{SD}{SC} = \frac{SB}{SO}.$$ Tiếp theo, ta chứng minh $AP \parallel DC$. Ta có $\angle BSA = 90^{\circ}$ và $\angle BSC = \angle DSC$ nên tam giác $BSD$ vuông cân tại $S$. Do đó $SM = NS$. Khi đó, ta có: $$\frac{SM}{SB} = \frac{NS}{NB} = \frac{1}{2}.$$ Từ đó ta suy ra $\frac{SC}{SO} = \frac{1}{2}$, hay $SO = 2SC$. Áp dụng định lí Pythagore trong tam giác $SBO$ ta có: $SB = \sqrt{2}a$. Mặt khác, ta có $OM = \frac{1}{2}a$ và $OS = \frac{2}{3}SC = \frac{1}{3}a$, suy ra $BM = \frac{\sqrt{2}}{2}a$ và $BO = \frac{\sqrt{6}}{2}a$. Áp dụng định lí Pythagore trong tam giác $SDO$ ta có: $SD = \sqrt{6}a$. Mặt khác, ta có $ON = \frac{1}{2}a$ và $OS = \frac{2}{3}SC = \frac{1}{3}a$, suy ra $DN = \frac{\sqrt{2}}{2}a$ và $DO = \frac{\sqrt{6}}{2}a$. Ta có $AP \parallel DC$ khi và chỉ khi: $$\frac{BP}{PA} = \frac{AD}{DC} = \sqrt{2} - 1,$$ trong đó ta đã sử dụng tính chất hình học của hình vuông. Từ định lí Menelaus cho tam giác $ACD$, ta có: $$\frac{AD}{CD}\cdot \frac{CP}{PA}\cdot \frac{NB}{ND} = 1.$$ Do đó, ta có: $$\frac{BP}{PA} = \frac{AD}{CD}\cdot \frac{ND}{NB} = (\sqrt{2} - 1)\cdot \frac{\frac{1}{2}a}{\frac{\sqrt{2}}{2}a} = \frac{2 - \sqrt{2}}{2}.$$ Ta cũng có thể tính được $\frac{PM}{PN}$ bằng cách sử dụng định lí Menelaus cho tam giác $ANB$: $$\frac{AP}{PB}\cdot \frac{MB}{MN}\cdot \frac{SN}{SA} = 1,$$ từ đó ta có: $$\frac{PM}{PN} = \frac{SN}{SM}\cdot \frac{PB}{PA}\cdot \frac{MB}{NB} = \frac{2}{1}\cdot \frac{2 - \sqrt{2}}{2}\cdot \frac{\frac{\sqrt{2}}{2}a}{\frac{\sqrt{2}}{2}a} = \frac{1}{3}.$$ Vậy $\frac{PM}{PN} = \frac{1}{3}$, ta đã chứng minh được bài toán.
Cho hình chóp S.ABCD có đáy là hình thoi ABCD tâm O và có SA = SB = SC = SD. Chứng minh rằng:
a) Đường thẳng SO vuông góc với mặt phẳng (ABCD)
Xem chi tiết
Cho hình chóp S ABCD, có đáy là hình vuông tâm O, SA vuông góc với mặt phẳng (ABCD). Gọi H, I, K lần lượt là hình chiếu vuông góc của điểm A lên SB, SC, SD.
1.CMR : AH, AK cùng vuông góc với SC. Từ đó suy ra 3 đường thẳng AH, AI, AK cùng nằm trong một mặt phẳng.
2. Chứng minh rằng HK⊥(SAC) , HK ⊥ AI.
cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, SA=SC, SB=SD, SO=a. khoảng cách từ điểm A đến mặt phẳng (SBD) là a. tính góc giữa SC và mặt phẳng (ABCD)
Cho hình chóp S.ABCD, có đáy ABCD là hình vuông tâm O có cạnh bằng a,SA=a√3 và SA vuông góc với (ABCD) a,CMR:DC vuông góc với (SAD) b, Tính góc giữa đường thẳng SD và mặt phẳng (ABCD)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy. Gọi B_1; C_1; D_1 là hình chiếu vuông góc của A lên các cạnh SB, SC, SD.a) Chứng minh rằng B_1D_1 // BD và SC ⊥ (AB_1D_1)b) Chứng minh rằng các điểm A, B_1, C_1, D_1 đồng phẳng và tứ giácAB_1C_1D_1 nội tiếp đường tròn.c) Cho SAasqrt{2}. Tính góc giữa hai đường thẳng SB và AC_1.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy. Gọi \(B_1\); \(C_1\); \(D_1\) là hình chiếu vuông góc của A lên các cạnh SB, SC, SD.
a) Chứng minh rằng \(B_1D_1\) // BD và SC ⊥ (A\(B_1D_1\))
b) Chứng minh rằng các điểm A, \(B_1\), \(C_1\), \(D_1\) đồng phẳng và tứ giác
A\(B_1C_1D_1\) nội tiếp đường tròn.
c) Cho SA\(=a\sqrt{2}\). Tính góc giữa hai đường thẳng SB và A\(C_1\).
Cho hình chóp S.ABCD, có đáy ABCD là hình vuông cạnh a. SA ⊥ (ABCD). SA = a
a. Chứng minh rằng: Các mặt bên của hình chóp đã cho là các tam giác vuông
b. Dựng AM ⊥ SB (M ∈ SB), AN ⊥ SD (N ∈ SD). Chứng minh rằng SC ⊥ (AMN)
c. Gọi K là giao điểm của đường thẳng SC với (AMN). Chứng minh rằng tứ giác AMKN có các đường chéo vuông góc với nhau. Tính diện tích tứ giác đó theo a