Chứng minh rằng :
\(\lim\limits_{n\rightarrow+\infty}\int\limits^1_0x^n\sin\pi xdx=0\)
Bài 2: Tích phân
SK
SK
Chứng minh rằng hàm số \(f\left(x\right)\) cho bởi :
\(f\left(x\right)=\int\limits^x_0\dfrac{t}{\sqrt{1+t^4}}dt;x\in\mathbb{R}\) là hàm số chẵn
Hướng dẫn giải
Thảo luận (1)
SK
Giả sử hàm số fleft(xright) liên tục trên đoạn left[-a;aright]
Chứng minh rằng :
intlimits^a_{-a}fleft(xright)dxleft{{}begin{matrix}2intlimits^a_0fleft(xright)dx;nếuflàhàmchẵn0;nếuflàhàmlẻend{matrix}right.
Áp dụng để tính intlimits^2_{-2}lnleft(x+sqrt{1+x^2}right)dx
Đọc tiếp
Giả sử hàm số \(f\left(x\right)\) liên tục trên đoạn \(\left[-a;a\right]\)
Chứng minh rằng :
\(\int\limits^a_{-a}f\left(x\right)dx=\left\{{}\begin{matrix}2\int\limits^a_0f\left(x\right)dx;nếuflàhàmchẵn\\0;nếuflàhàmlẻ\end{matrix}\right.\)
Áp dụng để tính \(\int\limits^2_{-2}\ln\left(x+\sqrt{1+x^2}\right)dx\)
Hướng dẫn giải
Thảo luận (1)
Tham khảo:
Giả sử hàm số f(x) là hàm số chẵn trên đoạn [-a; a], ta có:
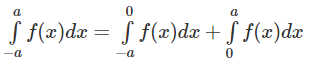
Đổi biến x = - t đối với tích phân
Ta được:
Vậy
Trường hợp sau chứng minh tương tự. Áp dụng:
Vì 
là hàm số lẻ trên đoạn [-2; 2] nên
SK
Giả sử hàm số \(f\left(x\right)\) liên tục trên đoạn \(\left[a;b\right]\). Chứng minh rằng :
\(\int\limits^{\dfrac{\pi}{2}}_0f\left(\sin x\right)dx=\int\limits^{\dfrac{\pi}{2}}_0f\left(\cos x\right)dx\)
SK
Đặt \(I_n=\int\limits^{\dfrac{\pi}{2}}_0\sin^nxdx;n\in\mathbb{N}^{\circledast}\)
a) Chứng minh rằng : \(I_n=\dfrac{n+1}{n}I_{n-2};n>2\)
b) Tính \(I_3\) và \(I_5\)
Hướng dẫn giải
Thảo luận (1)
a) Xét \(n>2\), ta có \(I_n=\int\limits^{\dfrac{\pi}{2}}_0\sin^{n-1}x.\sin xdx\)
SK
Đặt \(I_{m,n}=\int\limits^1_0x^m\left(1-x\right)^ndx;m,n\in\mathbb{N}^{\circledast}\)
Chứng minh rằng :
\(I_{m,n}=\dfrac{n}{m+1}I_{m+1,n-1};m>0,n>1\)
Từ đó tính \(I_{1,2}\) và \(I_{1,3}\) ?
SK
Hãy chỉ ra kết quả nào dưới đây đúng :
a) intlimits^{dfrac{pi}{2}}_0sin xdx+intlimits^{dfrac{3pi}{2}}_{dfrac{pi}{2}}sin xdx+intlimits^{2pi}_{dfrac{3pi}{2}}sin xdx0
b) intlimits^{dfrac{pi}{2}}_0left(sqrt[3]{sin x}-sqrt[3]{cos x}right)dx0
c) intlimits^{dfrac{1}{2}}_{-dfrac{1}{2}}lndfrac{1-x}{1+x}dx0
d) intlimits^2_0left(dfrac{1}{1+x+x^2+x^3}+1right)dx0
Đọc tiếp
Hãy chỉ ra kết quả nào dưới đây đúng :
a) \(\int\limits^{\dfrac{\pi}{2}}_0\sin xdx+\int\limits^{\dfrac{3\pi}{2}}_{\dfrac{\pi}{2}}\sin xdx+\int\limits^{2\pi}_{\dfrac{3\pi}{2}}\sin xdx=0\)
b) \(\int\limits^{\dfrac{\pi}{2}}_0\left(\sqrt[3]{\sin x}-\sqrt[3]{\cos x}\right)dx=0\)
c) \(\int\limits^{\dfrac{1}{2}}_{-\dfrac{1}{2}}\ln\dfrac{1-x}{1+x}dx=0\)
d) \(\int\limits^2_0\left(\dfrac{1}{1+x+x^2+x^3}+1\right)dx=0\)