Tính diện tích hình phẳng giới hạn bởi các đường :
a) \(y=x^2;y=x+2\)
b) \(y=\left|\ln x\right|;y=1\)
c) \(y=\left(x-6\right)^2;y=6x-x^2\)
Tính diện tích hình phẳng giới hạn bởi đường cong \(y=x^2+1\), tiếp tuyến với đường này tại điểm \(M\left(2;5\right)\) và trục Oy ?
Parabol \(y=\dfrac{x^2}{2}\) chia hình tròn có tâm tại gốc tọa độ, bán kính \(2\sqrt{2}\) thành hai phần. Tìm tỉ số diện tích của chúng ?
Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh trục Ox :
a) \(y=1-x^2;y=0\)
b) \(y=\cos x;y=0;x=0;x=\pi\)
c) \(y=\tan x;y=0;x=0;x=\dfrac{\pi}{4}\)
a) Phương trình hoành độ giao điểm
1 - x2 = 0 ⇔ x = ±1.
Thể tích cần tìm là :
b) Thể tích cần tìm là :
c) Thể tích cần tìm là :
.
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Đặt \(\widehat{POM}=\alpha;OM=R\left(0\le\alpha\le\dfrac{\pi}{3};R>0\right)\)
Gọi V là khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox (H.63)
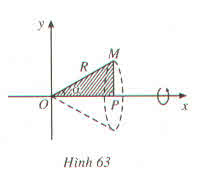
a) Tính thể tích của V theo \(\alpha\) và R
b) Tìm \(\alpha\) sao cho thể tích của V lớn nhất
a) Hoành độ điểm P là :
xp = OP = OM. cos α = R.cosα
Phương trình đường thẳng OM là y = tanα.x. Thể tích V của khối tròn xoay là:
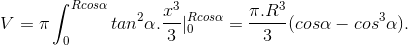
b) Đặt t = cosα => t ∈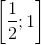 
. (vì α ∈ 
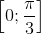), α = arccos t.
Ta có :
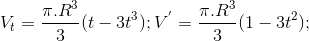
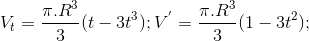
V' = 0 ⇔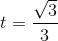
hoặc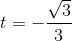 
(loại).
Từ đó suy ra V(t) lớn nhất ⇔ 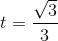, khi đó : 
.
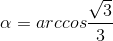Trả lời bởi Hiiiii~
Tính diện tích hình phẳng giới hạn bởi các đường sau :
a) \(y=2x-x^2;x+y=2\)
b) \(y=x^3-12x;y=x^2\)
c) \(x+y=1;x+y=-1;x-y=1;x-y=-1\)
d) \(y=\dfrac{1}{1+x^2};y=\dfrac{1}{2}\)
e) \(y=x^3-1\) và tiếp tuyến với \(y=x^3-1\) tại điểm \(\left(-1;-2\right)\)
Tính thể tích vật thể :
a) Có đáy là một tam giác cho bởi \(y=x;y=0;x=1\).Mỗi thiết diện vuông góc với trục Ox là một hình vuông
b) Có đáy là một hình tròn giới hạn bởi \(x^2+y^2=1\). Mỗi thiết diện vuông góc với trục Ox là một hình vuông
Tính thể tích các khối tròn xoay khi quay hình phẳng xác định bởi :
a) \(y=2-x^2;y=1\), quanh trục Ox
b) \(y=2x-x^2;y=x\), quanh trục Ox
c) \(y=\left(2x+1\right)^{\dfrac{1}{3}};x=0;y=3\), quanh trục Oy
d) \(y=x^2+1;x=0\) và tiếp tuyến với \(y=x^2+1\) tại điểm \(\left(1;2\right)\), quanh trục Ox
e) \(y=\ln x;y=0;x=e\), quanh trục Oy
Tính thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các đường \(y=\dfrac{1}{x};y=0;x=1;x=a\) (\(a>1\))
Gọi thể tích đó là \(V\left(a\right)\). Xác định thể tích của vật thể khi \(a\rightarrow+\infty\) (tức là \(\lim\limits_{a\rightarrow+\infty}V\left(a\right)\)
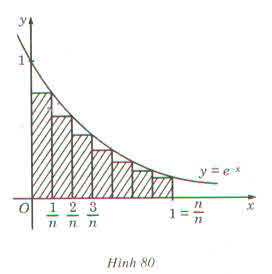
Một hình phẳng được giới hạn bởi \(y=e^{-x};y=0;x=0;x=1\)
Ta chia đoạn \(\left[0;1\right]\) thành n phần bằng nhau tạo thành một hình bậc thang (bởi n hình chữ nhật con như hình 80)
a) Tính diện tích \(S_n\) của hình bậc thang (tổng diện tích của n hình chữ nhật con)
b) Tìm \(\lim\limits_{n\rightarrow\infty}S_n\) và so sánh với cách tính diện tích hình phẳng này bằng công thức tính tích phân
Trả lời bởi Hai Binh