Cho hàm số \(y=ax^2\). Xác định hệ số a trong các trường hợp sau :
a) Đồ thị của nó đi qua điểm \(A\left(3;12\right)\)
b) Đồ thị của nó đi qua điểm \(B\left(-2;3\right)\)
Cho hàm số \(y=0,2x^2\)
a) Biết rằng điểm \(A\left(-2;b\right)\) thuộc đồ thị, hãy tính b. Điểm \(A'\left(2;b\right)\) có thuộc đồ thị của hàm số không ? Vì sao ?
b) Biết rằng điểm \(C\left(c;6\right)\) thuộc đồ thị, hãy tính c. Điểm \(D\left(c;-6\right)\) có thuộc đồ thị không ? Vì sao ?
a: Thay x=-2 và y=b vào (P), ta được:
\(b=\left(-2\right)^2\cdot0.2=0.8\)
Vì trong (P) thì f(x)=f(-x)
nên A'(2;0,8) thuộc (P)
b: Thay x=c và y=6 vào (P), ta được:
\(0,2c^2=6\)
nên \(c=\sqrt{30}\)
Vì trong (P) thì f(x)=f(-x) nên \(D\left(\sqrt{30};-6\right)\in\left(P\right)\)
Trả lời bởi Nguyễn Lê Phước ThịnhBiết rằng đường cong trong hình bên là một parabol y = ax2.
a) Tìm hệ số a.
b) Tìm tung độ của điểm thuộc parabol có hoành độ x = -3.
c) Tìm các điểm thuộc parabol có tung độ y = 8.
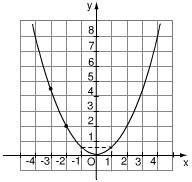
Bài giải:
a) Theo hình vẽ, ta lấy điểm A thuộc đồ thị có tọa độ là x = -2, y = 2. Khi đó ta được:
2 = a . (-2)2 suy ra a = 
b) Đồ thị có hàm số là y = x2 . Tung độ của điểm thuộc parabol có hoành độ x = -3 là y = (-3)2 suy ra y = 
.
c) Các điểm thuộc parabol có tung độ là 8 là:
8 = x2 ⇔ x2 = 16 ⇔ x = ± 4
Ta được hai điểm và tọa độ của hai điểm đó là M(4; 8) và M'(-4; 8).
Cho hàm số \(y=0,1x^2\)
a) Vẽ đồ thị của hàm số
b) Các điểm sau có thuộc đồ thị hay không : \(A\left(3;0,9\right),B\left(-5;2,5\right),C\left(-10;1\right)\)
a, - Đồ thị hàm số \(y=0,1x^2\)
b, Thay hoành độ điểm A vào phương trình hàm số:
\(y=0,1.3^2=0,1.9=0,9=yA\)
Vậy điểm A (3; 0,9) thuộc đồ thị hàm số.
Thay hoành độ điểm B vào phương trình hàm số:
\(y=0,1.\left(-5\right)^2=0,1.25=2,5=yB\)
Vậy điểm B (-5; 2,5) thuộc đồ thị hàm số.
Thay hoành độ điểm C vào phương trình hàm số:
\(y=0,1.\left(-10\right)^2=0,1.100=10\ne yc\)
Vậy điểm C (-10; 10) không thuộc đồ thị hàm số.
Cho hai hàm số \(y=\dfrac{1}{3}x^2\) và \(y=-x+6.\)
a) Vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ các giao điểm của hai đồ thị đó.
Bài giải:
Vẽ đồ thị: y = 
x2
|
x |
-6 |
-3 |
0 |
3 |
6 |
|
y = |
12 |
3 |
0 |
3 |
12 |
y = -x + 6
- Cho x = 0 => y = 6.
- Cho y = 0 => x = 6.
Vẽ đồ thị: xem hình bên dưới.
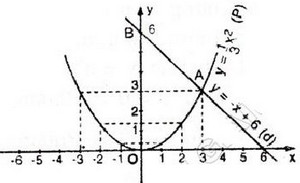
b) Giá trị gần đúng của tọa độ câc giao điểm (thực ra đây là giá trị đúng).
Hai đồ thị cắt nhau tại hai điểm A và B.
Theo đồ thị ta có A(3; 3) và B(-6; 12).
Trên mặt phẳng tọa độ (hình bên) có điểm M thuộc đồ thị của hàm số y = ax2.
a) Tìm hệ số a.
b) Điểm A(4;4) có thuộc đồ thị không?
c) Hãy tìm thêm hai điểm nữa (không kể điểm O) để vẽ đồ thị.
a) Theo hình vẽ ta có tọa độ của điểm M là x = 2, y = 1. M(2; 1) thuộc đồ thị hàm số y = ax2nên ta có: 1 = a . 22 ⇔ a = 
b) Theo câu a, ta có hàm số là y = x2.
Thay tọa độ của điểm A vào hàm số ta được 4 = x2 hay 4 = 4, thỏa mãn.
Vật điểm A(4; 4) có thuộc đồ thị hàm số y = x2.
c) Nhờ tính đối xứng của đồ thị, chẳng hạn ta lấy thêm hai điểm M'(-2; 1) và
A'(-4; 4). Vẽ đồ thị: xem hình bên dưới.
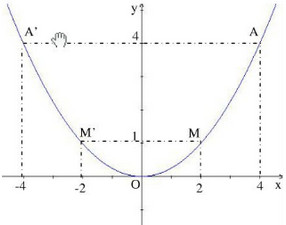
Xem thêm tại: http://loigiaihay.com/bai-7-trang-38-sgk-toan-9-tap-2-c44a5724.html#ixzz4dH3TtGWu
Cho ba hàm số: \(y=\dfrac{1}{2}x^2;y=x^2;y=2x^2.\)
a) Vẽ đồ thị của ba hàm số này trên cùng một mặt phẳng tọa độ.
b) Tìm ba điểm A, B ,C có cùng hoành độ x = -1,5 theo thứ tự nằm trêm ba đồ thị. Xác định tung độ tương ứng của chúng.
c) Tìm ba điểm A'; B';C' có cùng hoành độ x = 1,5 theo thứ tự nằm trên ba đồ thị. Kiểm tra tính đối xứng của A và A'; B và B'; C và C'.
d) Với mỗi hàm số trên, hãy tìm giá trị của x để hàm số đó có giá trị nhỏ nhất.
a) Vẽ đồ thị
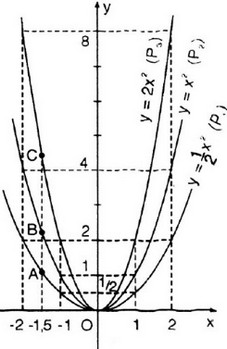
b) Gọi yA, yB, yC lần lượt là tung độ các điểm A, B, C có cùng hoành độ x = -1,5. Ta có:
yA = 
. (-1,5)2 = . 2,25 = 1,125
yB = (-1,5)2 = 2,25
yC = 2 (-1,5)2 = 2 . 2,25 = 4,5
c) Gọi yA, yB, yC’ lần lượt là tung độ các điểm A', B', C' có cùng hoành độ x = 1,5. Ta có:
yA, = . 1,52 = . 2,25 = 1,125
yB, = 1,52 = 2,25
yC’ = 2 . 1,52 = 2 . 2,25 = 4,5
Kiểm tra tính đối xứng: A và A', B và B', C và C' đối xứng với nhau qua trục tung Oy.
d) Với mỗi hàm số đã cho ta đều có hệ số a > 0 nên O là điểm thấp nhất của đồ thị. Khi đó ta có x = 0.
Vậy x = 0 thì hàm số có giả trị nhỏ nhất.
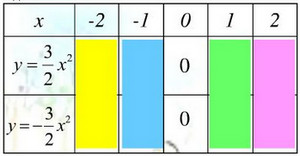
Cho hai hàm số: \(y=\dfrac{3}{2}x^2;y=-\dfrac{3}{2}x^2.\) Điền vào những ô trống của các bảng sau rồi vẽ hai đồ thị trên cùng một mặt phẳng tọa độ.
| x | -2 | -1 | 0 | 1 | 2 |
| \(y=\dfrac{3}{2}x^2\) |
| x | -2 | -1 | 0 | 1 | 2 |
| \(y=-\dfrac{3}{2}x^2\) |
Nhận xét về tính đối xứng của hai đồ thị đối với trục Ox.
Bài giải:
Thực hiện phép tính và điền vào chỗ trống ta được bảng sau:
Vẽ đồ thị:
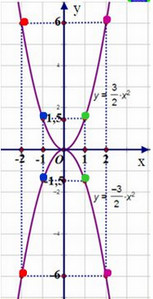
Nhận xét: Đồ thị của hai hàm số đối xứng với nhau qua trục Ox.
Xem thêm tại: http://loigiaihay.com/bai-4-trang-36-sgk-toan-9-tap-2-c44a5695.html#ixzz4dH45gBuO
Cho hàm số: \(y=f\left(x\right)=x^2.\)
a) Vẽ đồ thị của hàm số đó.
b) Tính các giá trị f(-8); f(-1;3); f(-0,75); f(1,5).
c) Dùng đồ thị để ước lượng các giá trị (0,5)2; (-1,5)2; (2,5)2.
d) Dùng đồ thị để ước lượng vị trí các điểm trên trục hoành biểu diễn các số \(\sqrt{3};\sqrt{7}.\)
a) Vẽ đồ thị hàm số y = x2.
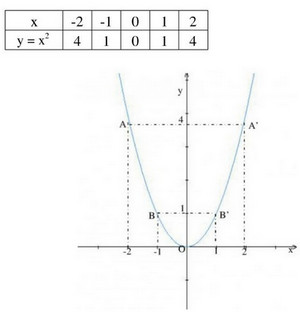
b) Ta có y = f(x) = x2 nên
f(-8) = (-8)2 = 64; f(-1,3) = (-1,3)2 = 1,69; f(-0,75) = (-0,75)2 = 0,5625; f(1,5) = 1,52 = 2,25.
c) Theo đồ thị ta có:
(0,5)2 ≈ 0,25
(-1,5)2 ≈ 2,25
(2,5)2 ≈ 6,25
d) Theo đồ thị ta có: Điểm trên trục hoành √3 thì có tung độ là y = (√3)2 = 3. Suy ra điểm biểu diễn √3 trên trục hoành bằng 1,7. Tương tự điểm biểu diễn √7 gồm bằng 2,7.
Cho hàm số y = -0,75x2. Qua đồ thị của hàm số đó, hãy cho biết khi x tăng từ -2 đến 4 thì giá trị nhỏ nhất và giá trị lớn nhất của y là bao nhiêu?
Vẽ đồ thị: y = -0,75x2
| x | -4 | -2 | -1 | 0 | 1 | 2 | 4 |
| y=-0,75x2 | -12 | -3 | -0,75 | 0 | -0,75 | -3 | -12 |
Vì -2 < 0 < 4 và khi x = 0 thì y = 0 là giá trị lớn nhất của hàm số. Hơn nữa khi x = -2 thì y = -0,75 . (-2)2 = -3, khi x = 4 thì y = -0,75 . (4)2 = -12 < -3
Do đó khi -2 ≤ x ≤ 4 thì giá trị nhỏ nhất của hàm số là -12 còn giá trị lớn nhất là 0.
Trả lời bởi Quốc Đạt
a: Thay x=3 và y=12 vào y=ax2, ta được:
9a=12
hay a=4/3
b: Thay x=-2 và y=3 vào \(y=ax^2\), ta được:
4a=3
hay a=3/4
Trả lời bởi Nguyễn Lê Phước Thịnh