Giải thích vì sao nếu f’(x) không đổi dấu qua \({x_0}\) thì \({x_0}\) không phải là điểm cực trị của hàm số f(x)?
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Bài 1. Tính đơn điệu và cực trị của hàm số
QL
Hướng dẫn giải
Thảo luận (1)
QL
Tìm cực trị của các hàm số sau:
a) \(y = {x^4} - 3{x^2} + 1\);
b) \(y = \frac{{ - {x^2} + 2x - 1}}{{x + 2}}\).
Hướng dẫn giải
Thảo luận (1)
a) Tập xác định của hàm số là \(\mathbb{R}\).
Ta có: \(y' = 4{x^3} - 6x,y' = 0 \Leftrightarrow 4{x^3} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \frac{{\sqrt 6 }}{2}\end{array} \right.\);
Bảng biến thiên:
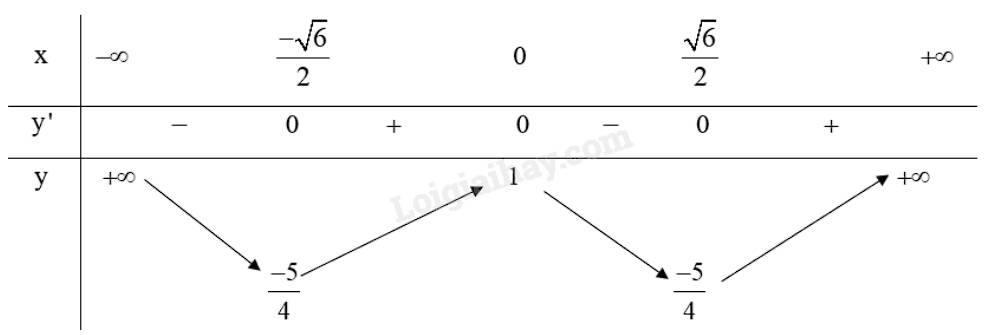
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại \(x = 0\) và .
Hàm số đạt cực tiểu tại \(x = \pm \frac{{\sqrt 6 }}{2}\) và \({y_{CT}} = \frac{{ - 5}}{4}\).
b) Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Ta có: \(y' = \frac{{\left( { - 2x + 2} \right)\left( {x + 2} \right) - \left( { - {x^2} + 2x - 1} \right)}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{ - {x^2} - 4x + 5}}{{{{\left( {x + 2} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 5\\x = 1\end{array} \right.\) (thỏa mãn)
Lập bảng biến thiên của hàm số:
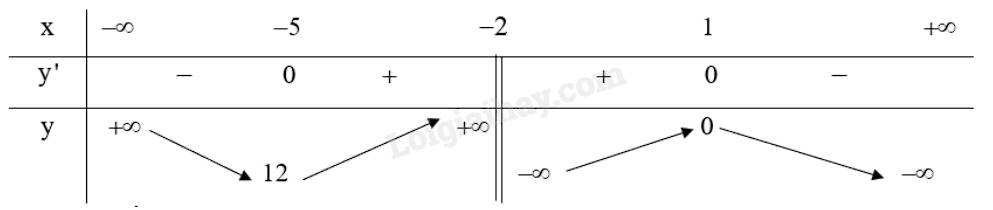
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại \(x = 1\) và .
Hàm số đạt cực tiểu tại \(x = - 5\) và \({y_{CT}} = 12\).
Trả lời bởi Hà Quang Minh
QL
Một vật được phóng thẳng đứng lên trên từ độ cao 2m với vận tốc ban đầu là 24,5m/s. Trong Vật lí, ta biết rằng khi bỏ qua sức cản của không khí thì độ cao h (mét) của vật sau t (giây) được cho bởi công thức: \(h\left( t \right) = 2 + 24,5t - 4,9{t^2}\). Hỏi tại thời điểm nào thì vật đạt độ cao lớn nhất?
Hướng dẫn giải
Thảo luận (1)
Xét hàm số: \(h\left( t \right) = 2 + 24,5t - 4,9{t^2}\).
Tập xác định của hàm số là \(\mathbb{R}\).
Ta có: \[h'\left( t \right) = - 9,8t + 24,5;h'\left( t \right) = 0 \Leftrightarrow - 9,8t + 24,5 = 0 \Leftrightarrow t = \frac{5}{2}\].
Bảng biến thiên:
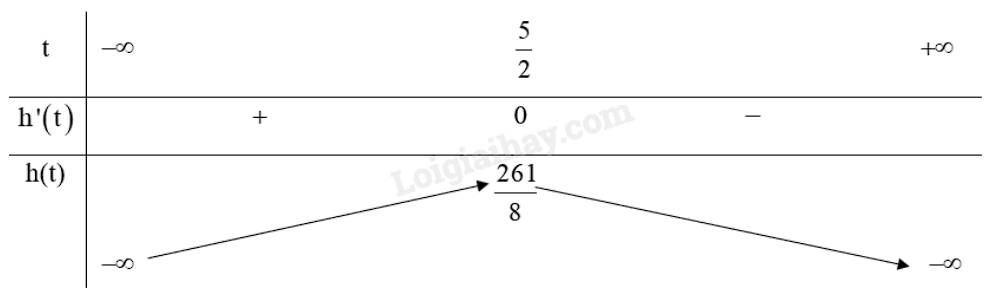
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại \(t = \frac{5}{2}\),
Vậy thời điểm vật đạt độ cao lớn nhất là \(t = \frac{5}{2}\) giây
Trả lời bởi Hà Quang Minh
QL
Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau:
a) Đồ thị hàm số \(y = {x^3} - \frac{3}{2}{x^2}\) (H.1.11);
b) Đồ thị hàm số \(y = \sqrt[3]{{{{\left( {{x^2} - 4} \right)}^2}}}\) (H.1.12).
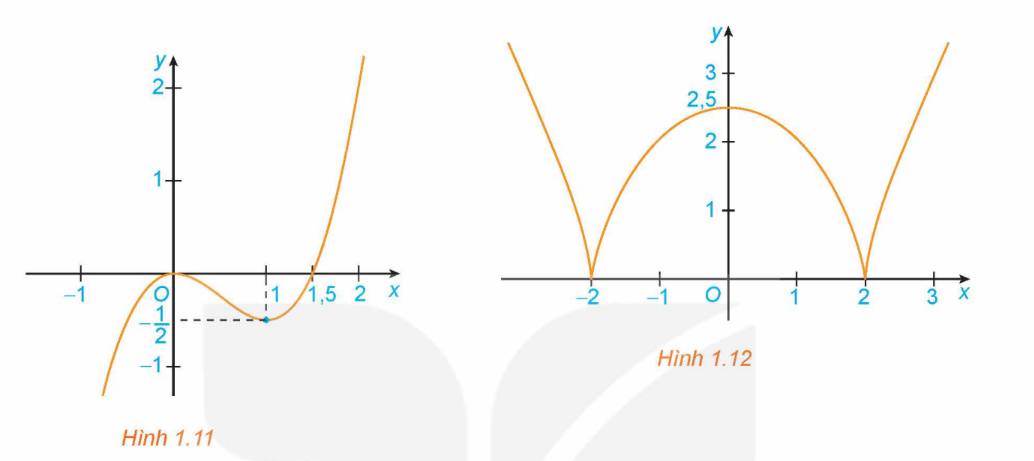
Hướng dẫn giải
Thảo luận (1)
a) Hàm số \(y = {x^3} - \frac{3}{2}{x^2}\) đồng biến trên \(\left( { - \infty ;0} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số \(y = {x^3} - \frac{3}{2}{x^2}\) nghịch biến trên \(\left( {0;1} \right)\).
b) Hàm số \(y = \sqrt[3]{{{{\left( {{x^2} - 4} \right)}^2}}}\) đồng biến trên \(\left( { - 2;0} \right)\) và \(\left( {2; + \infty } \right)\).
Hàm số \(y = \sqrt[3]{{{{\left( {{x^2} - 4} \right)}^2}}}\) nghịch biến trên \(\left( { - \infty ; - 2} \right)\) và \(\left( {0;2} \right)\).
Trả lời bởi Hà Quang Minh
QL
Xét sự đồng biến, nghịch biến của các hàm số sau:
a) \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x + 1\);
b) \(y = - {x^3} + 2{x^2} - 5x + 3\).
Hướng dẫn giải
Thảo luận (1)
a) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y' = {x^2} - 4x + 3,y' = 0 \Leftrightarrow {x^2} - 4x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\)
Lập bảng biến thiên của hàm số:
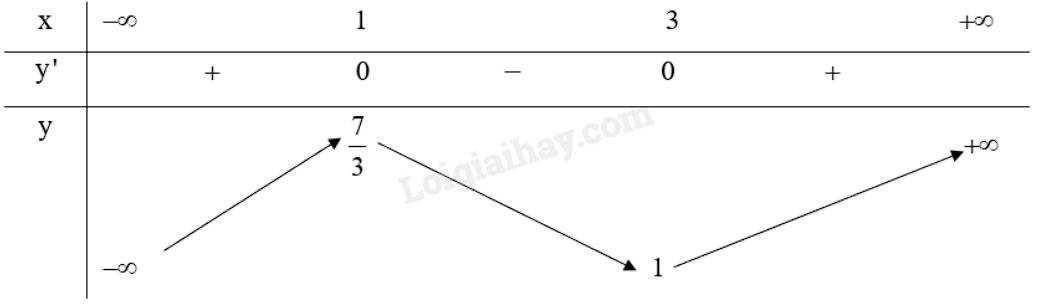
Hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x + 1\) đồng biến trên khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {3; + \infty } \right)\).
Hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x + 1\) nghịch biến trên khoảng \(\left( {1;3} \right)\).
b) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y' = - 3{x^2} + 4x - 5\)
Vì \( - 3{x^2} + 4x - 5 = - 3\left( {{x^2} - 2.\frac{2}{3} + \frac{4}{9}} \right) - \frac{{11}}{3} = - 3{\left( {x - \frac{2}{3}} \right)^2} - \frac{{11}}{3} < 0\;\forall x \in \mathbb{R}\)
Do đó, \(y' < 0\;\forall x \in \mathbb{R}\).
Vậy hàm số \(y = - {x^3} + 2{x^2} - 5x + 3\) nghịch biến trên \(\left( { - \infty ; + \infty } \right)\).
Trả lời bởi Hà Quang Minh
QL
Tìm các khoảng đơn điệu của các hàm số sau:
a) \(y = \frac{{2x - 1}}{{x + 2}}\);
b) \(y = \frac{{{x^2} + x + 4}}{{x - 3}}\).
Hướng dẫn giải
Thảo luận (1)
a) Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Ta có: \(y' = \frac{{2\left( {x + 2} \right) - \left( {2x - 1} \right)}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{2x + 4 - 2x + 1}}{{{{\left( {x + 2} \right)}^2}}} = \frac{5}{{\left( {x + 2} \right)}} > 0\;\forall x \ne - 2\)
Do đó, hàm số \(y = \frac{{2x - 1}}{{x + 2}}\) đồng biến trên \(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\).
b) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 3 \right\}\).
Ta có: \(y' = \frac{{\left( {{x^2} + x + 4} \right)'\left( {x - 3} \right) - \left( {{x^2} + x + 4} \right)\left( {x - 3} \right)'}}{{{{\left( {x - 3} \right)}^2}}} = \frac{{\left( {2x + 1} \right)\left( {x - 3} \right) - {x^2} - x - 4}}{{{{\left( {x - 3} \right)}^2}}} = \frac{{{x^2} - 6x - 7}}{{{{\left( {x - 3} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow \frac{{{x^2} - 6x - 7}}{{{{\left( {x - 3} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 7\\x = - 1\end{array} \right.\) (thỏa mãn)
Lập bảng biến thiên của hàm số:
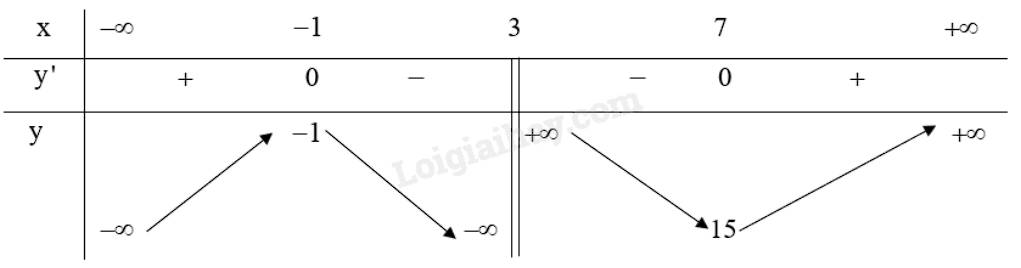
Từ bảng biến thiên ta thấy:
Hàm số \(y = \frac{{{x^2} + x + 4}}{{x - 3}}\) nghịch biến trên khoảng \(\left( { - 1;3} \right)\) và \(\left( {3;7} \right)\).
Hàm số \(y = \frac{{{x^2} + x + 4}}{{x - 3}}\) đồng biến trên khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {7; + \infty } \right)\).
Trả lời bởi Hà Quang Minh
QL
Xét chiều biến thiên của các hàm số sau:
a) \(y = \sqrt {4 - {x^2}} \);
b) \(y = \frac{x}{{{x^2} + 1}}\).
Hướng dẫn giải
Thảo luận (1)
a) Tập xác định: \(D = \left[ { - 2;2} \right]\).
Ta có: \(y' = \frac{{\left( {4 - {x^2}} \right)'}}{{2\sqrt {4 - {x^2}} }} = \frac{{ - x}}{{\sqrt {4 - {x^2}} }},y' = 0 \Leftrightarrow x = 0\left( {tm} \right)\)
Lập bảng biến thiên của hàm số:
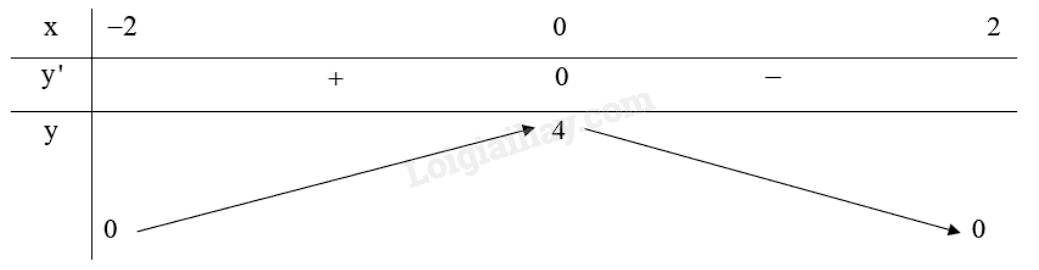
Hàm số \(y = \sqrt {4 - {x^2}} \) đồng biến trên khoảng \(\left( { - 2;0} \right)\).
Hàm số \(y = \sqrt {4 - {x^2}} \) nghịch biến trên khoảng \(\left( {0;2} \right)\).
b) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y' = \frac{{\left( {{x^2} + 1} \right) - 2x.x}}{{{{\left( {{x^2} + 1} \right)}^2}}} = \frac{{{x^2} + 1 - 2{x^2}}}{{{{\left( {{x^2} + 1} \right)}^2}}} = \frac{{ - {x^2} + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}},y' = 0 \Leftrightarrow \frac{{ - {x^2} + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\)
Lập bảng biến thiên của hàm số:
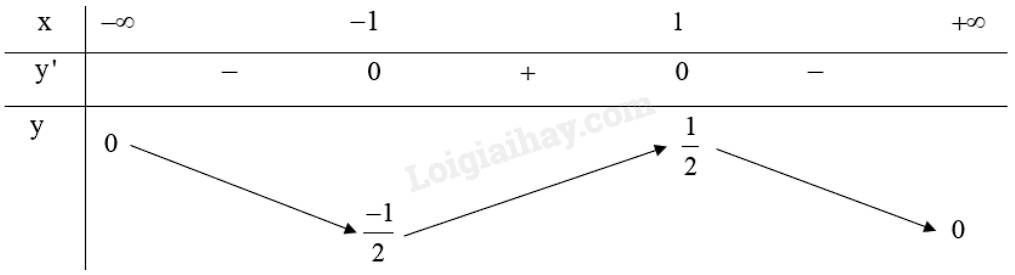
Hàm số \(y = \frac{x}{{{x^2} + 1}}\) nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\), \(\left( {1; + \infty } \right)\).
Hàm số \(y = \frac{x}{{{x^2} + 1}}\) đồng biến trên khoảng \(\left( { - 1;1} \right)\).
Trả lời bởi Hà Quang Minh
QL
Giả sử số dân của một thị trấn sau t năm kể từ năm 2000 được mô tả bởi hàm số Nleft( t right) frac{{25t + 10}}{{t + 5}},t ge 0, trong đó N(t) được tính bằng nghìn người.a) Tính số dân của thị trấn đó vào các năm 2000 và 2015.b) Tính đạo hàm N’(t) và mathop {lim }limits_{t to + infty } Nleft( t right). Từ đó giải thích tại sao dân số của thị trấn đó luôn tăng nhưng sẽ không vượt qua một ngưỡng nào đó.
Đọc tiếp
Giả sử số dân của một thị trấn sau t năm kể từ năm 2000 được mô tả bởi hàm số \(N\left( t \right) = \frac{{25t + 10}}{{t + 5}},t \ge 0\), trong đó N(t) được tính bằng nghìn người.
a) Tính số dân của thị trấn đó vào các năm 2000 và 2015.
b) Tính đạo hàm N’(t) và \(\mathop {\lim }\limits_{t \to + \infty } N\left( t \right)\). Từ đó giải thích tại sao dân số của thị trấn đó luôn tăng nhưng sẽ không vượt qua một ngưỡng nào đó.
Hướng dẫn giải
Thảo luận (1)
a) Dân số của thị trấn đó vào năm 2000 là: \(N\left( 0 \right) = \frac{{25.0 + 10}}{{0 + 5}} = \frac{{10}}{5} = 2\) (nghìn người)
Dân số của thị trấn đó vào năm 2015 là: \(N\left( {15} \right) = \frac{{25.15 + 10}}{{15 + 5}} = 19,25\) (nghìn người)
b) Ta có: , \(\mathop {\lim }\limits_{t \to + \infty } N\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } \frac{{25t + 10}}{{t + 5}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{25 + \frac{{10}}{t}}}{{1 + \frac{5}{t}}} = 25\)
Vì \(\mathop {\lim }\limits_{t \to + \infty } N\left( t \right) = 25\) và nên dân số của thị trấn đó luôn tăng nhưng sẽ không vượt qua ngưỡng 25 nghìn người.
Trả lời bởi Hà Quang Minh
QL
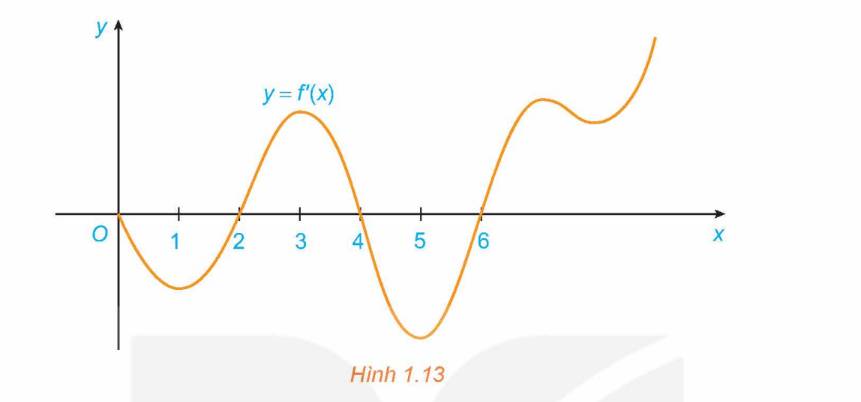
Đồ thị của đạo hàm bậc nhất \(y = f'\left( x \right)\) của hàm số f(x) được cho trong Hình 1.13:
a) Hàm số f(x) đồng biến trên những khoảng nào? Giải thích.
b) Tại giá trị nào của x thì f(x) có cực đại hoặc cực tiểu? Giải thích.
Hướng dẫn giải
Thảo luận (1)
a) Vì \(f'\left( x \right) > 0\) khi \(x \in \left( {2;4} \right)\) và \(x \in \left( {6; + \infty } \right)\). Do đó, hàm số f(x) đồng biến trên \(\left( {2;4} \right)\) và \(\left( {6; + \infty } \right)\).
Vì \(f'\left( x \right) < 0\) khi \(x \in \left( {0;2} \right)\) và \(x \in \left( {4;6} \right)\). Do đó, hàm số f(x) nghịch biến trên \(\left( {0;2} \right)\) và \(\left( {4;6} \right)\).
b) Vì \(f'\left( x \right) < 0\) với mọi \(x \in \left( {0;2} \right)\) và \(f'\left( x \right) > 0\) với mọi \(x \in \left( {2;4} \right)\) thì \(x = 2\) là một điểm cực tiểu của hàm số f(x).
Vì \(f'\left( x \right) > 0\) với mọi \(x \in \left( {2;4} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {4;6} \right)\) thì điểm \(x = 4\) là một điểm cực đại của hàm số f(x).
Vì \(f'\left( x \right) < 0\) với mọi \(x \in \left( {4;6} \right)\) và \(f'\left( x \right) > 0\) với mọi \(x \in \left( {6; + \infty } \right)\) thì điểm \(x = 6\) là một điểm cực tiểu của hàm số f(x).
Trả lời bởi Hà Quang Minh
QL
Tìm cực trị của các hàm số sau:
a) \(y = 2{x^3} - 9{x^2} + 12x - 5\);\(y = {x^4} - 4{x^2} + 2\)
b) \(y=x^4-4x^2+2\);
c) \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\);
d) \(y = \sqrt {4x - 2{x^2}} \).
Hướng dẫn giải
Thảo luận (1)
a) Tập xác định: \(D = \mathbb{R}\).
\(y' = 6{x^2} - 18x + 12\), \(y' = 0 \Leftrightarrow 6{x^2} - 18x + 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\)
Bảng biến thiên:
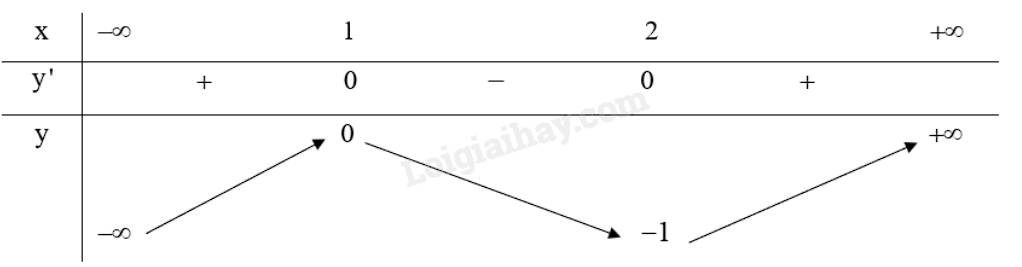
Từ bảng biến thiên ta có:
Hàm số \(y = 2{x^3} - 9{x^2} + 12x - 5\) có điểm cực đại là \(\left( {1;0} \right)\).
Hàm số \(y = 2{x^3} - 9{x^2} + 12x - 5\) có điểm cực tiểu là \(\left( {2; - 1} \right)\).
b) Tập xác định của hàm số là \(\mathbb{R}\).
Ta có: \(y' = 4{x^3} - 8x,y' = 0 \Leftrightarrow 4{x^3} - 8x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 2 \end{array} \right.\)
Bảng biến thiên:
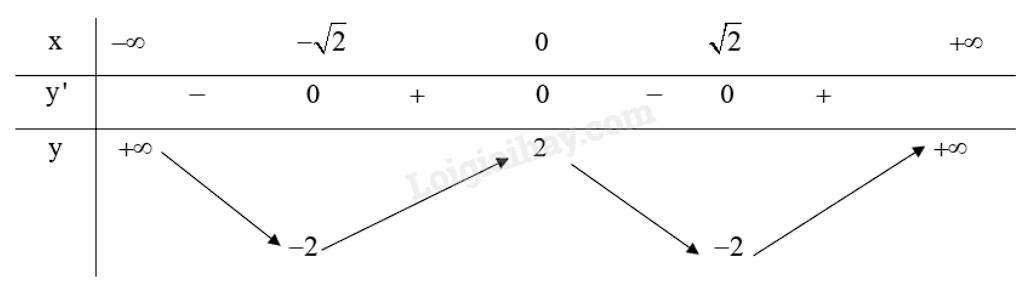
Từ bảng biến thiên ta có:
Hàm số \(y = {x^4} - 4{x^2} + 2\) đạt cực đại tại \(x = 0\) và .
Hàm số \(y = {x^4} - 4{x^2} + 2\) đạt cực tiểu tại \(x = \pm \sqrt 2 \) và \({y_{CT}} = - 2\).
c) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).
Ta có: \(y' = \frac{{\left( {2x - 2} \right)\left( {x - 1} \right) - \left( {{x^2} - 2x + 3} \right)}}{{{{\left( {x - 1} \right)}^2}}} = \frac{{{x^2} - 2x - 1}}{{{{\left( {x - 1} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 - \sqrt 2 \\x = 1 + \sqrt 2 \end{array} \right.\) (thỏa mãn)
Lập bảng biến thiên của hàm số:
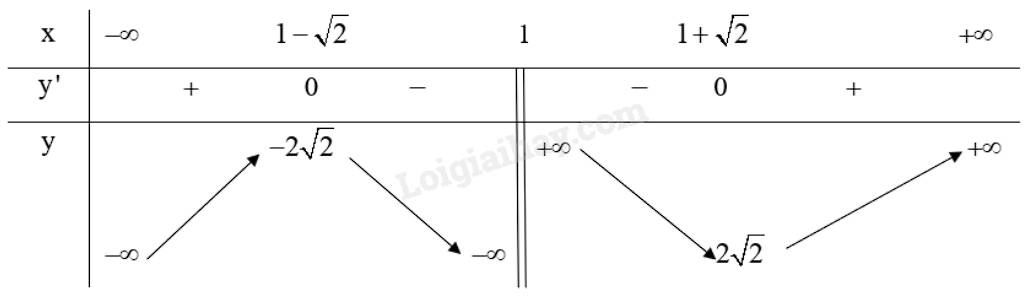
Từ bảng biến thiên ta có:
Hàm số \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\) đạt cực đại tại \(x = 1 - \sqrt 2 \) và .
Hàm số \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\) đạt cực tiểu tại \(x = 1 + \sqrt 2 \) và \({y_{CT}} = 2\sqrt 2 \).
d) \(y = \sqrt {4x - 2{x^2}} \)
Tập xác định: \(D = \left[ {0;2} \right]\).
Ta có: \(y' = \frac{{\left( {4x - 2{x^2}} \right)'}}{{2\sqrt {4x - 2{x^2}} }} = \frac{{ - x + 1}}{{\sqrt {4x - 2{x^2}} }},y' = 0 \Leftrightarrow x = 1\left( {tm} \right)\)
Ta có bảng biến thiên của hàm số:
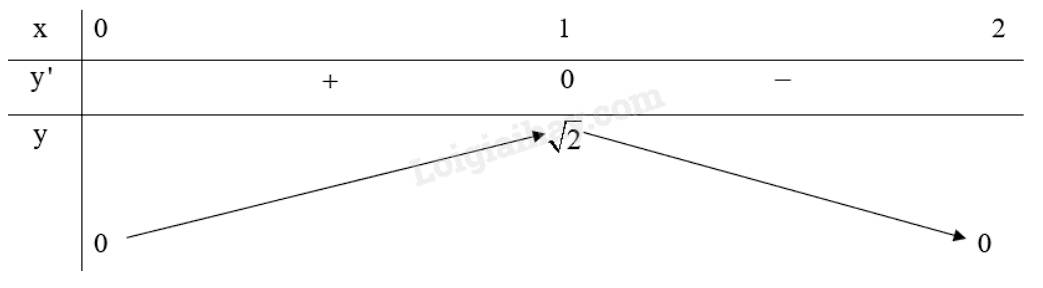
Do đó, hàm số đạt cực đại tại \(x = 1\), , hàm số không có cực tiểu.
Trả lời bởi Hà Quang Minh
Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Nếu f’(x) không đổi dấu qua \({x_0}\) thì:
TH1: \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\), ta có bảng biến thiên:
Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Nếu f’(x) không đổi dấu qua \({x_0}\) thì:
TH1: \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\), ta có bảng biến thiên:
Do đó, \({x_0}\) không phải là điểm cực trị của hàm số f(x).
Trả lời bởi Hà Quang Minh