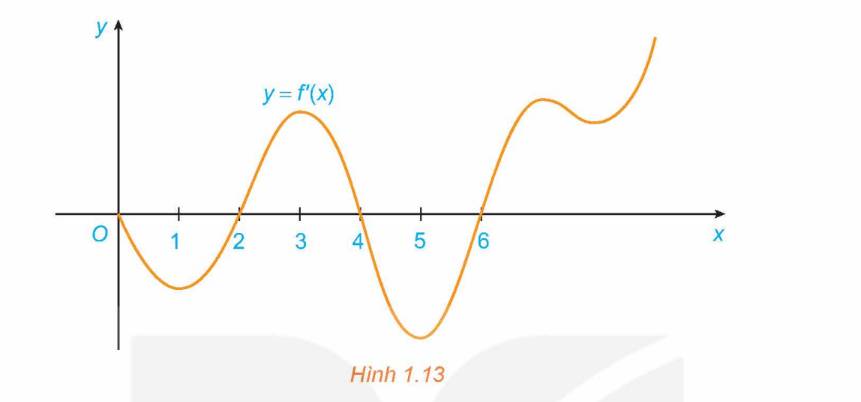
a) Vì \(f'\left( x \right) > 0\) khi \(x \in \left( {2;4} \right)\) và \(x \in \left( {6; + \infty } \right)\). Do đó, hàm số f(x) đồng biến trên \(\left( {2;4} \right)\) và \(\left( {6; + \infty } \right)\).
Vì \(f'\left( x \right) < 0\) khi \(x \in \left( {0;2} \right)\) và \(x \in \left( {4;6} \right)\). Do đó, hàm số f(x) nghịch biến trên \(\left( {0;2} \right)\) và \(\left( {4;6} \right)\).
b) Vì \(f'\left( x \right) < 0\) với mọi \(x \in \left( {0;2} \right)\) và \(f'\left( x \right) > 0\) với mọi \(x \in \left( {2;4} \right)\) thì \(x = 2\) là một điểm cực tiểu của hàm số f(x).
Vì \(f'\left( x \right) > 0\) với mọi \(x \in \left( {2;4} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {4;6} \right)\) thì điểm \(x = 4\) là một điểm cực đại của hàm số f(x).
Vì \(f'\left( x \right) < 0\) với mọi \(x \in \left( {4;6} \right)\) và \(f'\left( x \right) > 0\) với mọi \(x \in \left( {6; + \infty } \right)\) thì điểm \(x = 6\) là một điểm cực tiểu của hàm số f(x).