Đố :
a) Vẽ hình hoa bốn cánh : Hình hoa bốn cánh trên hình 60 được tạo bởi các cung có tâm A, B, C, D (trong đó A, B, C, D là các đỉnh của một hình vuông và tâm của cung là tâm của đường tròn chứa cung đó). Hãy vẽ lại hình 60

b) Vẽ lọ hoa : Chiếc lọ hoa trên hình 61 được vẽ trên giấy kẻ ô vuông bởi năm cung có tâm A, B, C, D, E. Hãy vẽ lại h

.png)
.png)



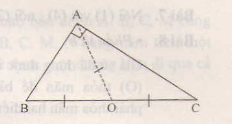

a) Vẽ hình vuông ABCD. Vẽ bốn cung tròn vào trong hình vuông, mỗi cung có tâm là một đỉnh của hình vuông và có bán kính bằng cạnh hình vuông.
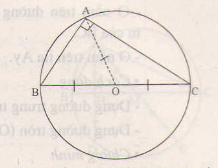
b) Vẽ 5 cung tròn có tâm lần lượt là A, B, C, D, E, bán kính bằng đường chéo của mỗi ô vuông.
Trả lời bởi Nhật Linh