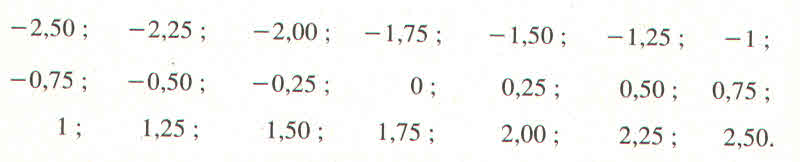
Cho hàm số \(y=f\left(x\right)=1,2x\). Tính các giá trị tương ứng của y khi cho x các giá trị sau đây, rồi lập bảng giá trị tương ứng giữa x và y :
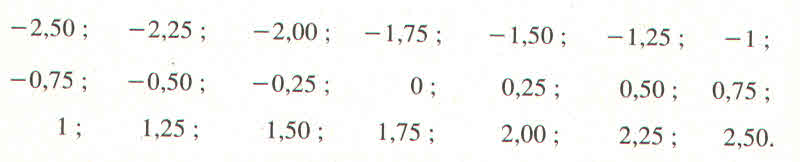
Cho hàm số \(y=f\left(x\right)=\dfrac{3}{4}x\). Tính :
\(f\left(-5\right)\) \(f\left(-4\right)\) \(f\left(-1\right)\) \(f\left(0\right)\)
\(f\left(\dfrac{1}{2}\right)\) \(f\left(1\right)\) \(f\left(4\right)\) \(f\left(2\right)\)
\(f\left(a\right)\) \(f\left(a+1\right)\)
a) Vẽ đồ thị của hàm số \(y=x\) và \(y=2x\) trên cùng một mặt phẳng tọa độ Oxy (h.5)
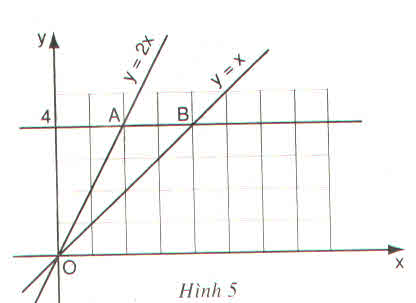
b) Đường thẳng song song với trục Ox và cắt Oy tại điểm có tung độ \(y=4\) lần lượt cắt các đường thẳng \(y=2x,y=x\) tại hai đểm A và B
Tìm tọa độ của các điểm A, B và tính chu vi, diện tích của tam giác OAB theo đơn vị đo trên các trục tọa độ là cm ?
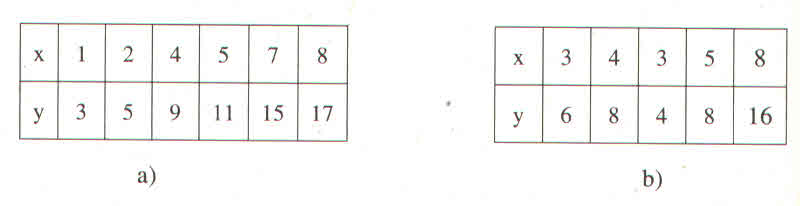
Trong các bảng sau ghi các giá trị tương ứng của \(x\) và \(y\). Bảng nào xác định \(y\) là hàm số của \(x\) ? Vì sao ?
Cho các hàm số \(y=0,5x\) và \(y=0,5x+2\)
a) Tính giá trị y tương ứng của mỗi hàm số theo giá trị đã cho của biến x rồi điền vào bảng sau :
| \(x\) | -2,5 | -2,25 | -1,5 | -1 | 0 | 1 | 1,5 | 2,25 | 2,5 |
| \(y=0,5x\) | |||||||||
| \(y=0,5x+2\) |
b) Có nhận xét gì về các giá trị tương ứng của hai hàm số đó khi biến x lấy cùng một giá trị ?
a) Sau khi tính giá trị của mỗi giá trị theo các giá trị của x đã cho ta được bảng sau:
b)Nhận xét: Cùng một giá trị của biến x, giá trị của hàm số y = 0,5x + 2 luôn luôn lớn hơn giá trị tương ứng của hàm số y = 0,5x là hai đơn vị.
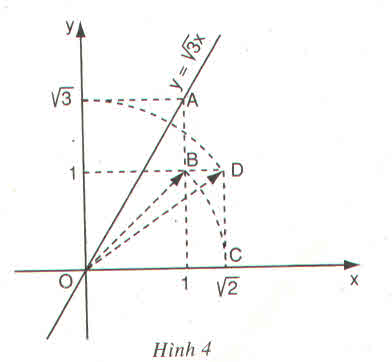
Trả lời bởi Lưu Hạ VyĐồ thị hàm số \(y=\sqrt{3}x\) được vẽ bằng compa và thước thẳng ở hình 4
Hãy tìm hiểu và trình bày lại các bước thực hiện vẽ đồ thị
Cho hàm số \(y=-\dfrac{1}{2}x+3\)
a) Tính các giá trị tương ứng của y theo các giá trị của x rồi điền vào bảng sau :
| \(x\) | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 |
| \(y=-\dfrac{1}{2}x+3\) |
b) Hàm số đã cho là hàm số đồng biến hay nghịch biến ? Vì sao ?
a)
Với y = -1/2x + 3, ta có f(-2,5) = -1/2(-2,5) + 3 = (2,5 + 6)/2 = 4,25;
Tương tự: f(-2) = 4; f(-1,5) = 3,75 ; f(-1) = 3,5 ; f(-0,5) = 3,25; f(0) = 3; f(0,5) = 2,75; f(1) = 2,5 ; f(1,5) = 2,25 ; f(2) = 2 ; f(2,5) = 1,75.
b) Hàm số nghịch biến vì khi x tăng lên thì y giảm đi.
Xem thêm tại: http://loigiaihay.com/bai-2-trang-45-sgk-toan-9-tap-1-c44a4307.html#ixzz4ezVwgGJL
a) Cho hàm số :
\(y=f\left(x\right)=\dfrac{2}{3}x\)
Tính :
\(f\left(-2\right);f\left(-1\right);f\left(0\right);f\left(\dfrac{1}{2}\right);f\left(1\right);f\left(2\right)\)
b) Cho hàm số :
\(y=g\left(x\right)=\dfrac{2}{3}x+3\)
Tính :
\(g\left(-2\right);g\left(-1\right);g\left(0\right);g\left(\dfrac{1}{2}\right);g\left(1\right);g\left(2\right)\)
c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lấy cùng một giá trị ?
c) Từ kết quả câu a, b ta được bảng sau:
Nhận xét:
- Các hàm số y = f(x) = 2/3 x và y = g(x) = 2/3 x + 3 là hai hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng lên.
- Cùng một giá trị của biến x, giá trị của hàm số y = g(x) luôn luôn lớn hơn giá trị tương ứng của hàm số y = f(x) là 3 đơn vị.
Trả lời bởi Lưu Hạ VyCho hai hàm số \(y=2x\) và \(y=-2x\)
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho
b) Trong hai hàm số đã cho, hàm số nào đồng biến ? Hàm số nào nghịch biến ? Vì sao ?
a) Trên mặt phẳng tọa độ Oxy. Với hàm số y = 2x cho x = 1 ta được y = 2, điểm A(1; 2) thuộc đồ thị y = 2x. Với hàm số y = -2x cho x = 1 ta được y = -2, điểm B(1; -2) thuộc đồ thị hàm số y = -2x, nên đường thẳng OB là đồ thị của hàm số y = -2x.
b) Ta có O(x1 = 0, y1 = 0) và A(x2 = 1, y2 = 2) thuộc đồ thị hàm số y = 2x, nên với x1 < x2 ta được f(x1) < f(x2).
Vậy hàm số y = 2x đồng biến trên R.
Lại có O(x1 = 0, y1 = 0) và B(x3 = 1, y3 = -2) thuộc đồ thị hàm số y = -2x, nên với x1 < x3 ta được f(x1) < f(x3).
Vậy hàm số y = -2x nghịch biến trên R.
Trả lời bởi Lưu Hạ VyCho hàm số \(y=f\left(x\right)=3x\)
Cho \(x\) hai giá trị bất kì \(x_1,x_2\) sao cho \(x_1< x_2\)
Hãy chứng minh \(f\left(x_1\right)< f\left(x_2\right)\) rồi rút ra kết luận hàm số đã cho đồng biến trên \(\mathbb{R}\)
Trả lời bởi Nguyen Thuy Hoa