Tìm \(x\) trong Hình 20.
Bài 1. Định lí Thalès trong tam giác
QL
Tìm x trong Hình 20.
Đọc tiếp
Hướng dẫn giải
Thảo luận (1)
QL
Đo chiều cao AB của một tòa nhà bằng hai cây cọc FE,DK, một sợi dây và một thước cuộn như sau:- Đặt cọc FE cố định, di chuyển cọc DK sao cho nhìn thấy K,F,A thẳng hàng.- Căng thẳng dây FC đi qua K và cắt mặt đất tại C.- Đo khoảng cách BC và DC trên mặt đất.Cho biết DK 1m,BC 24m,DC 1,2m. Tính chiều cao AB của tòa nhà.
Đọc tiếp
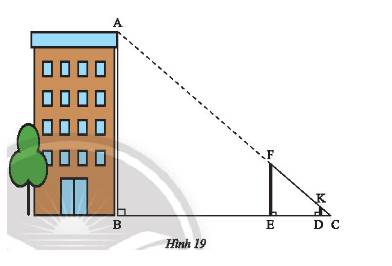
Đo chiều cao \(AB\) của một tòa nhà bằng hai cây cọc \(FE,DK\), một sợi dây và một thước cuộn như sau:
- Đặt cọc \(FE\) cố định, di chuyển cọc \(DK\) sao cho nhìn thấy \(K,F,A\) thẳng hàng.
- Căng thẳng dây \(FC\) đi qua \(K\) và cắt mặt đất tại \(C\).
- Đo khoảng cách \(BC\) và \(DC\) trên mặt đất.
Cho biết \(DK = 1m,BC = 24m,DC = 1,2m\). Tính chiều cao \(AB\) của tòa nhà.
Hướng dẫn giải
Thảo luận (1)
Vì \(\left\{ \begin{array}{l}KD \bot BC\\AB \bot BC\end{array} \right. \Rightarrow KD//AB\).
Xét tam giác \(CAB\) có \(KD//AB \Rightarrow \frac{{KD}}{{AB}} = \frac{{DC}}{{BC}}\) (hệ quả của định lí Thales).
\( \Rightarrow \frac{1}{{AB}} = \frac{{1,2}}{{24}} \Rightarrow AB = \frac{{24.1}}{{1,2}} = 20m\)
Vậy chiều cao \(AB\) của tòa nhà là 20m.
Trả lời bởi Hà Quang Minh
QL
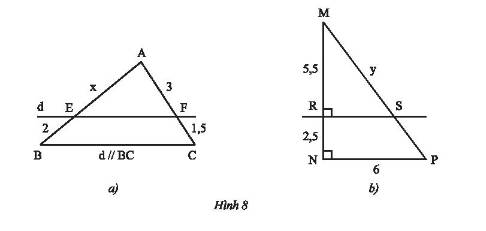
Tính độ dài \(x;y\) trong Hình 8.
Hướng dẫn giải
Thảo luận (1)
a)
Xét tam giác \(ABC\) có \(d//BC\) mà \(d\) cắt \(AB;AC\) lần lượt tại \(E\) và \(F\)nên theo định lí Thales ta có:
\(\frac{{AE}}{{BE}} = \frac{{AF}}{{CF}} \Rightarrow \frac{x}{2} = \frac{3}{{1,5}}\). Do đó, \(x = \frac{{2.3}}{{1,5}} = 4\).
Vậy \(x = 4\).
b) Ta có: \(MN = NR + MR = 2,5 + 5,5 = 8\)
Xét tam giác \(MNP\) vuông tại \(N\) ta có:
\(M{N^2} + N{P^2} = M{P^2}\)
\({8^2} + {6^2} = M{P^2}\)
\(100 = M{P^2} \Rightarrow MP = \sqrt {100} = 10\)
Xét tam giác \(MNP\) có \(\left\{ \begin{array}{l}RS \bot MN\\NP \bot MN\end{array} \right. \Rightarrow RS//NP\) (quan hệ từ vuông góc đến song song) nên theo định lí Thales ta có:
\(\frac{{MR}}{{MN}} = \frac{{MS}}{{MP}} \Rightarrow \frac{{5,5}}{8} = \frac{y}{{10}}\). Do đó, \(y = \frac{{5,5.10}}{8} = 6,875\).
Vậy \(y = 6,875\).
Trả lời bởi Hà Quang Minh
QL
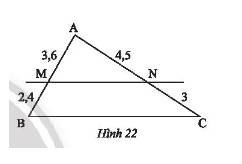
Quan sát Hình 22, chứng minh rằng \(MN//BC\).
Hướng dẫn giải
Thảo luận (2)
Ta có:
\(\frac{{AM}}{{MB}} = \frac{{3,6}}{{2,4}} = \frac{3}{2}\);\(\frac{{AN}}{{NC}} = \frac{{4,5}}{3} = \frac{3}{2}\).
Vì \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}} = \frac{3}{2}\)
Theo định lí Thales đảo trong \(\Delta ABC\), ta có \(MN//BC\) (điều phải chứng minh).
Trả lời bởi Hà Quang Minh
QL
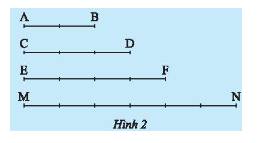
So sánh tỉ số của hai đoạn thẳng \(AB\) và \(CD\) với tỉ số của hai đoạn thẳng \(EF\) và \(MN\) trong Hình 2.
Hướng dẫn giải
Thảo luận (1)
Ta coi mỗi vạch chia là 1 đơn vị. Do đó, độ dài các đoạn thẳng là \(AB = 2\) đơn vị; \(CD = 3\) đơn vị; \(EF = 4\) đơn vị; \(MN = 6\) đơn vị.
Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{2}{3}\).
Tỉ số giữa hai đoạn thẳng \(EF\) và \(MN\) là \(EF:MN = \frac{{EF}}{{MN}} = \frac{4}{6} = \frac{2}{3}\).
Do đó, tỉ số của hai đoạn thẳng \(AB\) và \(CD\) bằng tỉ số của hai đoạn thẳng \(EF\) và \(MN\) .
Trả lời bởi Hà Quang Minh
QL
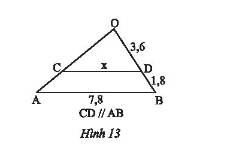
Tìm độ dài \(x\) trên Hình 13.
Hướng dẫn giải
Thảo luận (1)
Trong tam giác \(OAB\) có \(CD//AB\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{OD}}{{OB}} = \frac{{CD}}{{AB}}\) mà \(OB = OD + DB = 3,6 + 1,8 = 5,4\)
Suy ra, \(\frac{{3,6}}{{5,4}} = \frac{x}{{7,8}} \Rightarrow x = \frac{{3,6.7,8}}{{5,4}} = 5,2\).
Vậy \(x = 5,2\).
Trả lời bởi Hà Quang Minh
QL
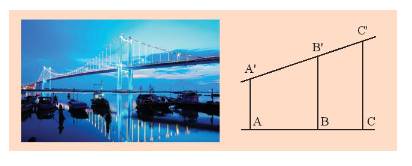
Những sợi cáp treo của cầu Thuận Phước (thuộc thành phố Đà Nẵng) cho ta hình ảnh những đoạn thẳng song song. Các đoạn thẳng song song \(AA',BB',CC'\) thể hiện ba sợi cáp của cầu. Nếu biết độ dài các đoạn \(AB,BC,A'B'\), có thể tính độ dài \(B'C'\) không?
Hướng dẫn giải
Thảo luận (1)
\(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}} \Rightarrow B'C' = \frac{{BC.A'B'}}{{AB}}\).
Trả lời bởi Hà Quang Minh
QL
Hãy tính tỉ số của hai đoạn thẳng \(AB\) và \(CD\) trong các trường hợp sau:
a) \(AB = 6cm;CD = 8cm\);
b) \(AB = 1,2m;CD = 42cm\).
Hướng dẫn giải
Thảo luận (1)
a) Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{6}{8} = \frac{3}{4}\).
b) Đổi \(1,2m = 120cm\)
Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{{120}}{{42}} = \frac{{20}}{7}\).
Trả lời bởi Hà Quang Minh
QL
Trên một tờ giấy kẻ cảo có các đường kẻ ngang song song và cách đều nhau.a) Vẽ một đường thẳng d cắt các đường kẻ ngang của tờ giấy như trong Hình 5a. Hãy so sánh độ dài các đoạn thẳng MN;NP;PQ và QE.b) Vẽ một tam giác ABC rồi vẽ một đường thẳng song song với cạnh BC và cắt hai cạnh AB,AC lần lượt tại B và C. Trên cạnh AB, lấy đoạn AI làm đơn vị đo tính tỉ số AB và BB; trên cạnh AC, lấy đoạn AJ làm đơn vị đo tính tỉ số AC và CC (Hình 5b).So sánh các tỉ số frac{{AB}}{{AB}} và frac{{AC}}{{AC}};fr...
Đọc tiếp
Trên một tờ giấy kẻ cảo có các đường kẻ ngang song song và cách đều nhau.
a) Vẽ một đường thẳng \(d\) cắt các đường kẻ ngang của tờ giấy như trong Hình 5a. Hãy so sánh độ dài các đoạn thẳng \(MN;NP;PQ\) và \(QE\).
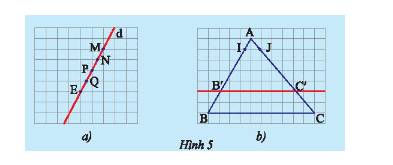
b) Vẽ một tam giác \(ABC\) rồi vẽ một đường thẳng song song với cạnh \(BC\) và cắt hai cạnh \(AB,AC\) lần lượt tại \(B'\) và \(C'\). Trên cạnh \(AB\), lấy đoạn \(AI\) làm đơn vị đo tính tỉ số \(AB'\) và \(BB'\); trên cạnh \(AC\), lấy đoạn \(AJ\) làm đơn vị đo tính tỉ số \(AC'\) và \(C'C\) (Hình 5b).
So sánh các tỉ số \(\frac{{AB'}}{{AB}}\) và \(\frac{{AC'}}{{AC}}\);\(\frac{{AB'}}{{B'B}}\) và \(\frac{{AC'}}{{C'C}}\);\(\frac{{B'B}}{{AB}}\) và \(\frac{{C'C}}{{AC}}\).
Hướng dẫn giải
Thảo luận (1)
a) Độ dài các đoạn thẳng \(MN;NP;PQ\) và \(QE\) đều bằng nhau vì chúng đều bằng độ dài đường chéo của một hình vuông nhỏ.
b) Trên cạnh \(AB\), lấy đoạn \(AI\) làm đơn vị đo nên độ dài \(AB' = 5AI;BB' = 2AI;\) Trên \(AB = 7AI\); cạnh \(AC\), lấy đoạn \(AJ\) làm đơn vị đo nên độ dài \(AC' = 5AJ;C'C = 2AJ\);\(AC = 7AJ\).
Tỉ số \(AB'\) và \(B'B\) là \(AB':B'B = \frac{{AB'}}{{B'B}} = \frac{{5AI}}{{2AI}} = \frac{5}{2}\);
Tỉ số \(AC'\) và \(C'C\) là \(AC':C'C = \frac{{AC'}}{{C'C}} = \frac{{5AJ}}{{2AJ}} = \frac{5}{2}\).
Do đó, \(\frac{{AB'}}{{B'B}} = \frac{{AC'}}{{C'C}} = \frac{5}{2}\).
Ta có: \(\frac{{AB'}}{{AB}} = \frac{{5AI}}{{7AI}} = \frac{5}{7};\frac{{AC'}}{{AC}} = \frac{{5AJ}}{{7AJ}} = \frac{5}{7}\).
Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{5}{7}\).
Ta có: \(\frac{{B'B}}{{AB}} = \frac{{2AI}}{{7AI}} = \frac{2}{7};\frac{{C'C}}{{AC}} = \frac{{2AJ}}{{7AJ}} = \frac{2}{7}\).
Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{2}{7}\).
Trả lời bởi Hà Quang Minh
QL
a) Hãy đo chiều dài và chiều rộng cái bàn học của em và tính tỉ số giữa hai kích thước này.
b) Quãng đường từ Thành phố Hồ Chí Minh đi Mỹ Tho là 70 km, quãng đường từ Thành phố Hồ Chí Minh đi Cà Mau là 350 km. Tính tỉ số giữa hai quãng đường này.
c) Cho biết \(\frac{{AB}}{{CD}} = \frac{3}{5}\) và \(AB = 6cm\). Hãy tính \(CD\).
Hướng dẫn giải
Thảo luận (1)
a) Chiều dài của cái bàn học của em là \(120cm\); chiều rộng của cái bàn học của em là \(70cm\). Tỉ số giữa chiều dài và chiều rộng của cái bàn là: \(CD:CR = \frac{{CD}}{{CR}} = \frac{{120}}{{70}} = \frac{{12}}{7}\).
b) Tỉ số giữa hai quãng đường từ Thành phố Hồ Chí Minh đi Mỹ Tho và từ Thành phố Hồ Chí Minh đi Cà Mau là: \(70:350 = \frac{{70}}{{350}} = \frac{1}{5}\).
c) Ta có: \(\frac{{AB}}{{CD}} = \frac{3}{5}\) mà \(AB = 6cm \Rightarrow \frac{6}{{CD}} = \frac{3}{5} \Rightarrow CD = \frac{{5.6}}{3} = 10cm\)
Vậy \(CD = 10cm\).
Trả lời bởi Hà Quang Minh
a) Xét tam giác \(ABC\) có \(MN//BC\) nên theo định lí Thales ta có:
\(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}} \Rightarrow \frac{x}{2} = \frac{{4,5}}{3}\). Do đó, \(x = \frac{{4,5.2}}{3} = 3\).
Vậy \(x = 3\).
b) Ta có: \(CD = AC + AD = 3 + 6 = 9\)
Xét tam giác \(CDE\) có \(AB//DE\) nên theo định lí Thales ta có:
\(\frac{{AC}}{{CD}} = \frac{{BC}}{{CE}} \Rightarrow \frac{3}{9} = \frac{{2,4}}{x}\). Do đó, \(x = \frac{{9.2,4}}{3} = 7,2\).
Vậy \(x = 7,2\).
c) Vì \(\left\{ \begin{array}{l}DE \bot PM\\MN \bot PM\end{array} \right. \Rightarrow DE//MN\) (quan hệ từ vuông góc đến song song).
\(PE + EN = 3,9 + 2,6 = 6,5\)
Xét tam giác \(PMN\) có \(DE//MN\) nên theo định lí Thales ta có:
\(\frac{{DM}}{{MP}} = \frac{{NE}}{{NP}} \Rightarrow \frac{x}{5} = \frac{{2,6}}{{6,5}}\). Do đó, \(x = \frac{{2,6.5}}{{6,5}} = 2\).
Vậy \(x = 2\).
Trả lời bởi Hà Quang Minh