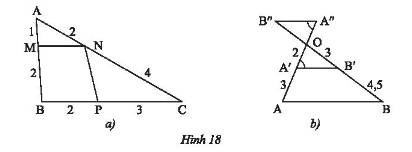
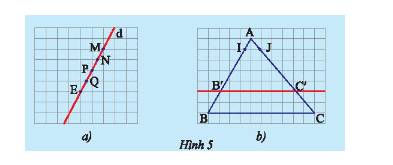
a) Xét tam giác \(ABC\) có \(MN//BC\) nên theo định lí Thales ta có:
\(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}} \Rightarrow \frac{x}{2} = \frac{{4,5}}{3}\). Do đó, \(x = \frac{{4,5.2}}{3} = 3\).
Vậy \(x = 3\).
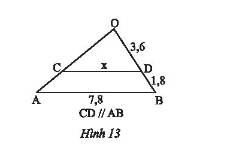
b) Ta có: \(CD = AC + AD = 3 + 6 = 9\)
Xét tam giác \(CDE\) có \(AB//DE\) nên theo định lí Thales ta có:
\(\frac{{AC}}{{CD}} = \frac{{BC}}{{CE}} \Rightarrow \frac{3}{9} = \frac{{2,4}}{x}\). Do đó, \(x = \frac{{9.2,4}}{3} = 7,2\).
Vậy \(x = 7,2\).
c) Vì \(\left\{ \begin{array}{l}DE \bot PM\\MN \bot PM\end{array} \right. \Rightarrow DE//MN\) (quan hệ từ vuông góc đến song song).
\(PE + EN = 3,9 + 2,6 = 6,5\)
Xét tam giác \(PMN\) có \(DE//MN\) nên theo định lí Thales ta có:
\(\frac{{DM}}{{MP}} = \frac{{NE}}{{NP}} \Rightarrow \frac{x}{5} = \frac{{2,6}}{{6,5}}\). Do đó, \(x = \frac{{2,6.5}}{{6,5}} = 2\).
Vậy \(x = 2\).