Bài 2. Đường trung bình của tam giác

Vì \(BD = DA \Rightarrow D\) là trung điểm của \(AB\);

Vì \(EC = EA \Rightarrow E\) là trung điểm của \(AC\).

Do đó, \(DE\) là đường trung bình của tam giác \(ABC\)

\( \Rightarrow \left\{ \begin{array}{l}DE//BC\\DE = \frac{1}{2}BC\end{array} \right. \Rightarrow 45 = \frac{1}{2}BC \Leftrightarrow BC = 45.2 = 90\left( m \right)\)

Vậy khoảng các của hai điểm \(B\) và \(C\) là 90 m.

Xét tam giác \(ABC\) có \(MN//BC\) nên áp dụng định lí Thales cho tam giác ta có:

\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\).

Mà \(M\) là trung điểm của \(AB\) nên \(AM = \frac{1}{2}BC\) hay \(\frac{{AM}}{{BC}} = \frac{1}{2}\).

Do đó, \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow \frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow AN = \frac{1}{2}AC\).

Do đó, \(N\) là trung điểm của \(AC\).

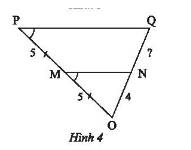
Từ hình vẽ ta có: \(\widehat {OMN} = \widehat {OPQ}\).

Mà hai góc này ở vị trí đồng vị nên \(MN//PQ\)

Xét tam giác \(OPQ\) có \(MN//PQ\) nên áp dụng định lí Thales cho tam giác ta có:

\(\frac{{OM}}{{MP}} = \frac{{ON}}{{NQ}} \Leftrightarrow \frac{5}{5} = \frac{4}{{NQ}} \Rightarrow NQ = \frac{{4.5}}{5} = 4\).

Vậy \(NQ = 4\).

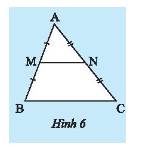
a) Vì \(AM = MB \Rightarrow M\) là trung điểm của \(AB\) (do \(M\) thuộc \(AB\))

\( \Rightarrow AM = \frac{1}{2}AB \Leftrightarrow \frac{{AM}}{{AB}} = \frac{1}{2}\);

Vì \(AN = NC \Rightarrow N\) là trung điểm của \(AC\) (do \(N\) thuộc \(AC\))

\( \Rightarrow AN = \frac{1}{2}AC \Leftrightarrow \frac{{AN}}{{AC}} = \frac{1}{2}\).

b) Vì \(\frac{{AM}}{{AB}} = \frac{1}{2};\frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\).

Xét tam giác \(ABC\) có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) nên áp dụng định lí Thales đảo ta được \(MN//BC\).

c) Xét tam giác \(ABC\) có \(MN//BC\) nên áp dụng hệ quả định lí Thales ta được \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\)

Mà \(\frac{{AM}}{{AB}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\).

Vậy \(\frac{{MN}}{{BC}} = \frac{1}{2}\) (điều phải chứng minh).

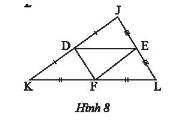
Xét ΔLJK có F,E lần lượt là trung điểm của LK,LJ

=>FE là đường trung bình

=>FE//KJ và FE=KJ/2=5cm

DJ=JK/2=5cm

Xét ΔJKL có KF/KL=KD/KJ

nên FD//LJ và FD/LJ=KF/KL=1/2

=>FD=3,7cm

Xét ΔABC có D,E lần lượt là trung điểm của AB,AC

=>DE là đường trung bình

=>DE=1/2BC

=>BC=2DE=90(m)

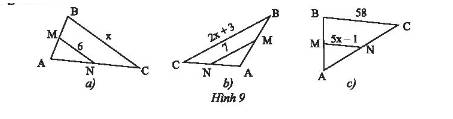
- Hình a:

Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:

\(\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}x \Leftrightarrow 6 = \frac{1}{2}x \Leftrightarrow x = 6:\frac{1}{2} = 12\)

- Hình b:

Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:

\(\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}\left( {x + 3} \right) \Leftrightarrow 7 = \frac{1}{2}\left( {x + 3} \right) \Leftrightarrow \left( {x + 3} \right) = 7:\frac{1}{2} = 14\)

\( \Rightarrow x = 14 - 3 \Leftrightarrow x = 11\).

- Hình c

Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:

\[\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}.58 \Leftrightarrow \left( {5x - 1} \right) = \frac{1}{2}.58\]

\[ \Leftrightarrow \left( {5x - 1} \right) = 29 \Leftrightarrow 5x = 30 \Leftrightarrow x = 30:5 \Leftrightarrow x = 6\].

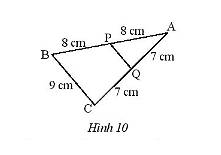
Xét ΔABC có P,Q lần lượt là trung điểm của AB,AC

=>PQ là đường trung bình

=>PQ=BC/2=4,5(cm)

Đoạn thẳng \(AB\) là đường chéo của hình chữ nhật với chiều dài là \(4cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(A{B^2} = {2^2} + {4^2} = 4 + 16 = 20 \Rightarrow AB = \sqrt {20}  = 2\sqrt 5 \)

Đoạn thẳng \(AC\) là đường chéo của hình chữ nhật với chiều dài là \(4cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(A{C^2} = {2^2} + {4^2} = 4 + 16 = 20 \Rightarrow AC = \sqrt {20}  = 2\sqrt 5 \)

Đoạn thẳng \(BC\) là đường chéo của hình chữ nhật với chiều dài là \(6cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(B{C^2} = {2^2} + {6^2} = 4 + 36 = 40 \Rightarrow BC = \sqrt {40}  = 2\sqrt {10} \)

Từ hình vẽ ta thấy:

\(Q\) là trung điểm của \(AC\);

\(R\) là trung điểm của \(AB\);

\(P\) là trung điểm của \(BC\).

- Vì \(Q\) là trung điểm của \(AC\); \(R\) là trung điểm của \(AB\) nên \(QR\) là đường trung bình của tam giác \(ABC \Rightarrow QR = \frac{1}{2}BC\) (tính chất đường trung bình)

\( \Leftrightarrow QR = \frac{1}{2}.2\sqrt {10}  = \sqrt {10} \left( {cm} \right)\).

- Vì \(Q\) là trung điểm của \(AC\); \(P\) là trung điểm của \(BC\) nên \(QP\) là đường trung bình của tam giác \(ABC \Rightarrow QP = \frac{1}{2}AB\) (tính chất đường trung bình)

\( \Leftrightarrow QP = \frac{1}{2}.2\sqrt 5  = \sqrt 5 \left( {cm} \right)\).

- \(R\) là trung điểm của \(AB\); \(P\) là trung điểm của \(BC\) nên \(RP\) là đường trung bình của tam giác \(ABC \Rightarrow RP = \frac{1}{2}AC\) (tính chất đường trung bình)

\( \Leftrightarrow RP = \frac{1}{2}.2\sqrt 5  = \sqrt 5 \left( {cm} \right)\).

a) Vì \(K\)là giao điểm của \(AF\) và \(DC\) nên \(K \in CD\).

Vì \(ABCD\) là hình thang nên \(AB//CD \Rightarrow AB//CK\).

Xét tam giác \(ABF\) có \(CK//AB\) ta có:

\(\frac{{FA}}{{FK}} = \frac{{FB}}{{FC}}\) (hệ quả của định lí Thales)

Mà \(F\) lần lượt là trung điểm \(BC\) nên \(\frac{{FB}}{{FC}} = 1 \Rightarrow \frac{{FA}}{{FK}} = 1 \Rightarrow FA = FK\)

Xét tam giác \(ABF\) và tam giác \(KCF\) có:

\(FB = FC\) (chứng minh trên)

\(FK = FA\) (chứng minh trên)

\(\widehat {{F_1}} = \widehat {{F_2}}\)

Do đó, tam giác \(ABF\) bằng tam giác \(KCF\) (c – g – c).

b) Vì \(E\) là trung điểm của \(AD\);\(F\) là trung điểm của \(BC\) nên \(EF\) là đường trung bình của tam giác \(ADK\).

Do đó, \(EF//DK\) (tính chất)\( \Rightarrow EF//DC\)

Mà \(AB//CD \Rightarrow EF//AB//CD\) (điều phải chứng minh).

c) Vì \(EF\) là đường trung bình của tam giác \(ADK\) nên \(EF = \frac{1}{2}DK\).

Tam giác \(ABF\) bằng tam giác \(KCF\) nên \(AB = CK\) (hai cạnh tương ứng)

Ta có: \(DK = DC + CK \Rightarrow DK = DC + AB\).

Do đó, \[EF = \frac{1}{2}DK = \frac{1}{2}\left( {DC + AB} \right) = \frac{{DC + AB}}{2}\] (điều phải chứng minh).