Bài 1. Định lí Thalès trong tam giác

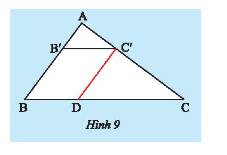
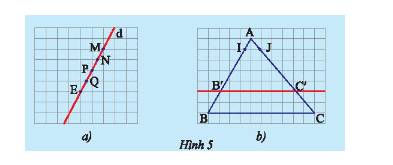
a) Xét tam giác \(ABC\) có \(B'C'//BC\) nên theo định lí Thales ta có:

\(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} \Rightarrow \frac{2}{6} = \frac{{AC'}}{8}\). Do đó, \(AC' = \frac{{2.8}}{6} = \frac{8}{3}\left( {cm} \right)\).

Vậy \(AC' = \frac{{16}}{3}cm\).

b) Xét tam giác \(ABC\) có \(C'D//AB\) nên theo định lí Thales ta có:

\(\frac{{BD}}{{BC}} = \frac{{AC'}}{{AC}} \Rightarrow \frac{{BD}}{{10}} = \frac{{\frac{8}{3}}}{8}\). Do đó, \(BD = \frac{{10.\frac{8}{3}}}{8} = \frac{{10}}{3}\left( {cm} \right)\).

Vậy \(BD = \frac{{10}}{3}cm\).

Ta có: \(BB' = AB - AB' = 6 - 2 = 4cm\)

Vì \(\left\{ \begin{array}{l}B'C'//BC\\C'D//AB\end{array} \right. \Rightarrow \left\{ \begin{array}{l}B'C'//BD\\C'D//B'B\end{array} \right.\) (do \(D \in BC;B' \in AB\))

Xét tứ giác \(B'C'DB\) có

\(\left\{ \begin{array}{l}B'C'//BD\\C'D//B'B\end{array} \right. \Rightarrow \) tứ giác \(B'C'DB\) là hình bình hành (dấu hiệu nhận biết)

\( \Rightarrow \left\{ \begin{array}{l}B'C' = BD = \frac{{10}}{3}cm\\BB' = C'D = 4cm\end{array} \right.\) (tính chất hình bình hành)

c) Ta có: \(\frac{{AB'}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AC'}}{{AC}} = \frac{{\frac{8}{3}}}{8} = \frac{1}{3};\frac{{BC'}}{{BC}} = \frac{{\frac{{10}}{3}}}{{10}} = \frac{1}{3}\)

Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{{B'C'}}{{BC}}\).

Trong tam giác \(OAB\) có \(CD//AB\).

Theo hệ quả của định lí Thales ta có:

\(\frac{{OD}}{{OB}} = \frac{{CD}}{{AB}}\) mà \(OB = OD + DB = 3,6 + 1,8 = 5,4\)

Suy ra, \(\frac{{3,6}}{{5,4}} = \frac{x}{{7,8}} \Rightarrow x = \frac{{3,6.7,8}}{{5,4}} = 5,2\).

Vậy \(x = 5,2\).

Ta xem độ dài một cạnh của hình vuông nhỏ là \(a\) và đường chéo của một hình vuông nhỏ là \(b\).

Khi đó, độ dài các đoạn thẳng là

\(AB = b;BC = 3b;A'B' = a;B'C' = 3a;AC = 4b;A'C' = 4a\)

a) Tỉ số của \(AB\) và \(BC\)là \(\frac{{AB}}{{BC}} = \frac{b}{{3b}} = \frac{1}{3}\).

Tỉ số của \(A'B'\) và \(B'C'\) là \(\frac{{A'B'}}{{B'C'}} = \frac{a}{{3a}} = \frac{1}{3}\).

Do đó, \(AB\) và \(BC\) tỉ lệ với \(A'B'\) và \(B'C'\).

b) Tỉ số của \(AC\) và \(A'C'\)là \(\frac{{AC}}{{A'C'}} = \frac{{4b}}{{4a}} = \frac{b}{a}\).

Tỉ số của \(AB\) và \(A'B'\) là \(\frac{{AB}}{{A'B'}} = \frac{b}{a}\).

Do đó, \(AC\) và \(A'C'\) tỉ lệ với \(AB\) và \(A'B'\).

a)

Xét tam giác \(ABC\) có \(d//BC\) mà \(d\) cắt \(AB;AC\) lần lượt tại \(E\) và \(F\)nên theo định lí Thales ta có:

\(\frac{{AE}}{{BE}} = \frac{{AF}}{{CF}} \Rightarrow \frac{x}{2} = \frac{3}{{1,5}}\). Do đó, \(x = \frac{{2.3}}{{1,5}} = 4\).

Vậy \(x = 4\).

b) Ta có: \(MN = NR + MR = 2,5 + 5,5 = 8\)

Xét tam giác \(MNP\) vuông tại \(N\) ta có:

\(M{N^2} + N{P^2} = M{P^2}\)

\({8^2} + {6^2} = M{P^2}\)

\(100 = M{P^2} \Rightarrow MP = \sqrt {100}  = 10\)

Xét tam giác \(MNP\) có \(\left\{ \begin{array}{l}RS \bot MN\\NP \bot MN\end{array} \right. \Rightarrow RS//NP\)  (quan hệ từ vuông góc đến song song) nên theo định lí Thales ta có:

\(\frac{{MR}}{{MN}} = \frac{{MS}}{{MP}} \Rightarrow \frac{{5,5}}{8} = \frac{y}{{10}}\). Do đó, \(y = \frac{{5,5.10}}{8} = 6,875\).

Vậy \(y = 6,875\).

Ta có:

\(AD = 1,5m;AE = 3m;BD = 3m;EC = 6m;\)

\(AB = AD + DB = 1,5 + 3 = 4,5m;AC = AE + EC = 3 + 6 = 9m\)

Ta có:

\(\frac{{AD}}{{BD}} = \frac{{1,5}}{3} = \frac{1}{2};\frac{{AE}}{{EC}} = \frac{3}{6} = \frac{1}{2}\). Do đó, \(AD\) và \(BD\) tỉ lệ với \(AE\) và \(EC\).

\(\frac{{AD}}{{AB}} = \frac{{1,5}}{{4,5}} = \frac{1}{3};\frac{{AE}}{{AC}} = \frac{3}{9} = \frac{1}{3}\). Do đó, \(AD\) và \(AB\) tỉ lệ với \(AE\) và \(AC\).

\(\frac{{AB}}{{BD}} = \frac{{4,5}}{3} = \frac{3}{2};\frac{{AC}}{{EC}} = \frac{9}{6} = \frac{3}{2}\). Do đó, \(AB\) và \(BD\) tỉ lệ với \(AC\) và \(EC\).

Ta coi mỗi vạch chia là 1 đơn vị. Do đó, độ dài các đoạn thẳng là \(AB = 2\) đơn vị; \(CD = 3\) đơn vị; \(EF = 4\) đơn vị; \(MN = 6\) đơn vị.

Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{2}{3}\).

Tỉ số giữa hai đoạn thẳng \(EF\) và \(MN\) là \(EF:MN = \frac{{EF}}{{MN}} = \frac{4}{6} = \frac{2}{3}\).

Do đó, tỉ số của hai đoạn thẳng \(AB\) và \(CD\) bằng tỉ số của hai đoạn thẳng \(EF\) và \(MN\) .

a) Tỉ số giữa hai số 5 và 8 là \(5:8 = \frac{5}{8}\).

b) Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD=\dfrac{AB}{CD}=\dfrac{3}{4}\)

\(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}} \Rightarrow B'C' = \frac{{BC.A'B'}}{{AB}}\).

a) Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{6}{8} = \frac{3}{4}\).

b) Đổi \(1,2m = 120cm\)

Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{{120}}{{42}} = \frac{{20}}{7}\).

a) Độ dài các đoạn thẳng \(MN;NP;PQ\) và \(QE\) đều bằng nhau vì chúng đều bằng độ dài đường chéo của một hình vuông nhỏ.

b) Trên cạnh \(AB\), lấy đoạn \(AI\) làm đơn vị đo nên độ dài \(AB' = 5AI;BB' = 2AI;\) Trên \(AB = 7AI\); cạnh \(AC\), lấy đoạn \(AJ\) làm đơn vị đo nên độ dài \(AC' = 5AJ;C'C = 2AJ\);\(AC = 7AJ\).

Tỉ số \(AB'\) và \(B'B\) là \(AB':B'B = \frac{{AB'}}{{B'B}} = \frac{{5AI}}{{2AI}} = \frac{5}{2}\);

Tỉ số \(AC'\) và \(C'C\) là \(AC':C'C = \frac{{AC'}}{{C'C}} = \frac{{5AJ}}{{2AJ}} = \frac{5}{2}\).

Do đó,  \(\frac{{AB'}}{{B'B}} = \frac{{AC'}}{{C'C}} = \frac{5}{2}\).

Ta có: \(\frac{{AB'}}{{AB}} = \frac{{5AI}}{{7AI}} = \frac{5}{7};\frac{{AC'}}{{AC}} = \frac{{5AJ}}{{7AJ}} = \frac{5}{7}\).

Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{5}{7}\).

Ta có: \(\frac{{B'B}}{{AB}} = \frac{{2AI}}{{7AI}} = \frac{2}{7};\frac{{C'C}}{{AC}} = \frac{{2AJ}}{{7AJ}} = \frac{2}{7}\).

Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{2}{7}\).