Biểu diễn hình học tập nghiệm của các hệ bất phương trình sau :
a) \(\left\{{}\begin{matrix}2x-1\le0\\-3x+5< 0\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}3-y< 0\\2x-3y+1>0\end{matrix}\right.\)
Biểu diễn hình học tập nghiệm của các hệ bất phương trình sau :
a) \(\left\{{}\begin{matrix}2x-1\le0\\-3x+5< 0\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}3-y< 0\\2x-3y+1>0\end{matrix}\right.\)
Biểu diễn hình học tập nghiệm của các bất phương trình sau :
a) \(3+2y>0\)
b) \(2x-1< 0\)
c) \(x-5y< 2\)
d) \(2x+y>1\)
e) \(-3x+y+2\le0\)
f) \(2x-3y+5\ge0\)
a) Vẽ đường thẳng \(3+2y=0\). Vì điểm O(0;0) có tọa độ thõa mãn bất phương trình nên phần không tô màu là miền nghiệm của bất phương trình:
Có 3 nhóm máy A, B, C dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản phẩm mỗi loại phải lần lượt dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được cho trong bảng sau

Một đơn vị sản phẩm I lãi 3 nghìn đồng, một đơn vị sản phẩm II lãi 5 nghìn đồng. Hãy lập phương án để việc sản xuất hai loại sản phẩm trên có lãi cao nhất ?
Gọi x là số đơn vị sản phẩm loại I, y là số đơn vị sản phẩm loại II được nhà máy lập kế hoạch sản xuất. Khi đó số lãi nhà máy nhân được là P = 3x + 5y (nghìn đồng).
Các đại lượng x, y phải thỏa mãn các điều kiện sau:
(I)
(II)
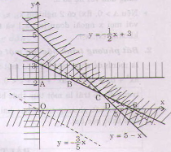
Miền nghiệm của hệ bất phương trình (II) là đa giác OABCD (kể cả biên).
Biểu thức F = 3x + 5y đạt giá trị lớn nhất khi (x; y) là tọa độ đỉnh C.
(Từ 3x + 5y = 0 => y = Các đường thẳng qua các đỉnh của OABCD và song song với đường y =
cát Oy tại điểm có tung độ lớn nhất là đường thẳng qua đỉnh C).
Phương trình hoành độ điểm C: 5 - x = <=> x = 4.
Suy ra tung độ điểm C là yc = 5 - 4 = 1. Tọa độ C(4; 1). Vậy trong các điều kiện cho phép của nhà máy, nếu sản xuất 4 đơn vị sản phẩm loại I và 1 đơn vị sản phẩm đơn vị loại II thì tổng số tiền lãi lớn nhất bằng:
Fc = 3.4 + 5.1 = 17 nghìn đồng.
Trả lời bởi Nguyễn Đắc ĐịnhBiểu diễn hình học tập nghiệm của các hệ bất phương trình bậc nhất hai ẩn sau :
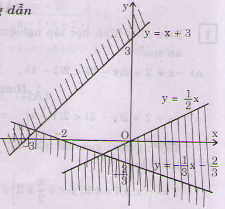
a. \(\left\{{}\begin{matrix}x-2y< 0\\x+3y>-2\\y-x< 3\end{matrix}\right.\)
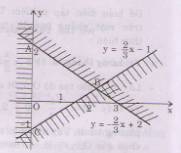
b. \(\left\{{}\begin{matrix}\dfrac{x}{3}+\dfrac{y}{2}-1< 0\\x+\dfrac{1}{2}-\dfrac{3y}{2}\le2\\x\ge0\end{matrix}\right.\)
a) <=>
Miền nghiệm của hệ bất phương trình là miền không bị gạch sọc ở hình bên (không kể các điểm).
b) <=>
Miền nghiệm của hệ bất phương trình là miền tam giác ABC bao gồm cả các điểm trên cạnh AC và cạnh BC (không kể các điểm của cạnh AB).
Trả lời bởi Nguyễn Đắc Định
Biểu diễn hình học tập nghiệm của các bất phương trình bậc nhất hai ẩn sau :
a. \(-x+2+2\left(y-2\right)< 2\left(1-x\right)\)
b. \(3\left(x-1\right)+4\left(y-2\right)< 5x-3\)
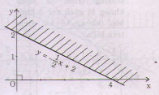
a) - x + 2 + 2(y - 2) < 2(1 - x) <=> y <
Tập nghiệm của bất phương trình là:
T = {(x, y)|x ∈ R; y < }.
Để biểu diễn tập nghiệm T trên mặt phẳng tọa độ, ta thực hiện:
+ Vẽ đường thẳng (d): y=
+ Lấy điểm gốc tọa độ O(0; 0) (d).
Ta thấy: 0 < - 0 + 2. Chứng tỏ (0; 0) là một nghiệm của bất phương trình. Vậy nửa mặt phẳng bờ là đường thẳng (d) (không kể bờ) chứa gốc O(0; 0) là tập hợp các điểm biểu diễn tập nghiệm của bất phương trình đã cho (nửa mặt phẳng không bị gạch sọc)
Trả lời bởi Nguyễn Đắc Định
a) \(\left\{{}\begin{matrix}2x-1\le0\\-3x+5< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\x>\dfrac{5}{3}\end{matrix}\right.\)\(\Leftrightarrow x\in\varnothing\).
Trả lời bởi Bùi Thị Vânb) Vẽ hai đường thẳng \(y=3;2x-3y+1=0\).
Vì điểm \(O\left(0;0\right)\) có tọa độ thỏa mãn bất phương trình \(2x-3y+1>0\) và không thỏa mãn bất phương trình \(3-y< 0\) nên phần không tô màu là miền nghiệm của hệ bất phương trình: \(\left\{{}\begin{matrix}3-y< 0\\2x-3y+1>0\end{matrix}\right.\).