a) <=>
Miền nghiệm của hệ bất phương trình là miền không bị gạch sọc ở hình bên (không kể các điểm).
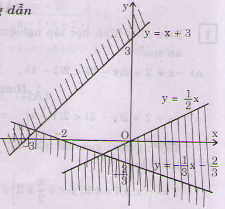
b) <=>
Miền nghiệm của hệ bất phương trình là miền tam giác ABC bao gồm cả các điểm trên cạnh AC và cạnh BC (không kể các điểm của cạnh AB).
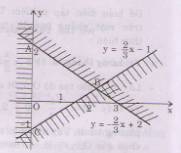
a) <=>
Miền nghiệm của hệ bất phương trình là miền không bị gạch sọc ở hình bên (không kể các điểm).

b) <=>
Miền nghiệm của hệ bất phương trình là miền tam giác ABC bao gồm cả các điểm trên cạnh AC và cạnh BC (không kể các điểm của cạnh AB).

Biểu diễn hình học tập nghiệm của các hệ bất phương trình sau :
a) \(\left\{{}\begin{matrix}2x-1\le0\\-3x+5< 0\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}3-y< 0\\2x-3y+1>0\end{matrix}\right.\)
1, số nghiệm nguyên của bất phương trình \(\left|\dfrac{2-3\left|x\right|}{1+x}\right|\le2\) là
a. 2 b.5 c.3 d.4
2, với giá trị nào của m thì 2 đường thẳng sau đây song song?
Δ1: \(\left\{{}\begin{matrix}x=8+\left(m+1\right)t\\y=10-t\end{matrix}\right.\) và Δ2 \(mx-6y-76=0\)
a. m=2 b. không có m thỏa mãn c. m=-3 d. m=2 hoặc m=-3
3, xác định vị trí tương đối của 2 đường thẳng
Δ1: \(\left\{{}\begin{matrix}x=2+5t\\y=3-6t\end{matrix}\right.\) và Δ2: \(\left\{{}\begin{matrix}x=-2+5t'\\y=-3+6t'\end{matrix}\right.\)
a. trùng nhau b. song song nhau c. vuông góc nhau d. cắt nhau nhưng không vuông góc
4, cho ΔABC có độ dài 3 cạnh là a,b,c. R là bán kính đường tròn ngoại tiếp tam giác. khẳng định nào sau đây đúng?
a, \(cosB=\dfrac{b^2+c^2-a^2}{2bc}\) b, \(\dfrac{a}{sinA}=R\) c, SΔABC \(=\dfrac{1}{2}abc\) d, \(m_c^2=\dfrac{2b^2+2a^2-c^2}{4}\)
5, Cho bpt 4x-3y-5≤0(1). chọn khẳng định đúng
a, bpt 1 có vô số nghiệm
b, ------- chỉ có 1 nghiệm duy nhất
c, ------- vô nghiệm
d, ------- có duy nhất 2 nghiệm
6, trong 1 cuộc thi pha chế, mỗi đội chơi đc sd tối đa 30g hương liệu, 12l nc và 180 gam đường để pha chế nước cam và táo
+) để pha chế 1l nước cam cần 20 gam đường, 1l nước và 1g hương liệu
+) -------------------------- táo ------- 10gam -------------------------- 4g ---------------
mỗi lít nước cam được 20 điểm thưởng, mỗi lít nước táo nhận được 50 điểm thưởng. hỏi cần chế bao nhiêu lít nước trái cây mỗi loại đạt được số điểm thưởng cao nhất?
A. 5l nước cam và 5l nước táo
B. 7l ------------------- 3l-------------
C 3l-------------------- 7l------------
D 6l ------------------- 6l------------
1. tìm tất cả các giá trị thực của tham số m để hàm số y= \(\sqrt{x-m}-\sqrt{6-2x}\) có tập xác định là một đoạn trên trục số
A. m=3 B=m<3 C. m>3 D. m<\(\frac{1}{3}\)
2. tìm tất cả các giá trị thực của hàm số y=\(\sqrt{m-2x}\)-\(\sqrt{x+1}\) có tập xác định là một đoạn trên trục số
A.m<-2 B.m>2 C. m>-\(\frac{1}{2}\) D. m>-2
3. bất phương trình nào sau đây tương đương với bất phương trình x+5>0
A. (x-1)2 (x+5) > 0 B. x2 (x+5) >0
C. \(\sqrt{x+5}\left(x+5\right)\)> 0 D. \(\sqrt{x+5}\left(x-5\right)\)>0
4. bất phương trình ax+b > 0 vô nghiệm khi
A.\(\left\{{}\begin{matrix}a\ne0\\b=0\end{matrix}\right.\) B.\(\left\{{}\begin{matrix}a>0\\b>0\end{matrix}\right.\)
C. \(\left\{{}\begin{matrix}a=0\\b\ne0\end{matrix}\right.\) D.\(\left\{{}\begin{matrix}a=0\\b\le0\end{matrix}\right.\)
5.bất phương trình ax+b>0 có tập nghiệm R khi
A.\(\left\{{}\begin{matrix}a=0\\b>0\end{matrix}\right.\) B.\(\left\{{}\begin{matrix}a>0\\b>0\end{matrix}\right.\)
C. \(\left\{{}\begin{matrix}a=0\\b\ne0\end{matrix}\right.\) D.\(\left\{{}\begin{matrix}a=0\\b\le0\end{matrix}\right.\)
6.bất phương trình ax+b \(\le\)0 vô nghiệm khi
A.\(\left\{{}\begin{matrix}a=0\\b>0\end{matrix}\right.\) B.\(\left\{{}\begin{matrix}a>0\\b>0\end{matrix}\right.\)
C. \(\left\{{}\begin{matrix}a=0\\b\ne0\end{matrix}\right.\) D.\(\left\{{}\begin{matrix}a=0\\b\le0\end{matrix}\right.\)
7.tập nghiệm S của bất phương trình \(5x-1\ge\frac{2x}{5}+3\) là
A. R B. (-∞; 2) C. (-\(\frac{5}{2}\); +∞) D. \([\frac{20}{23}\); +∞\()\)
MONG MỌI NGƯỜI GIẢI CHI TIẾT GIÚP EM Ạ TvT
giải các hệ BPT sau:
a) \(\left\{{}\begin{matrix}5x-2>4x+5\\5x-4< x+2\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}2x+1>3x+4\\5x+3\ge8x-9\end{matrix}\right.\)
c) \(\left\{{}\begin{matrix}\frac{5x+2}{3}\ge4-x\\\frac{6-5x}{13}< 3x+1\end{matrix}\right.\)
d) \(\left\{{}\begin{matrix}\frac{4x-5}{7}< x+3\\\frac{3x+8}{4}>2x-5\end{matrix}\right.\)
e) \(\left\{{}\begin{matrix}6x+\frac{5}{7}< 4x+7\\\frac{8x+3}{2}< 2x+5\end{matrix}\right.\)
f) \(\left\{{}\begin{matrix}15x-2>2x+\frac{1}{3}\\2\left(x-4\right)< \frac{3x-14}{2}\end{matrix}\right.\)
g) \(\left\{{}\begin{matrix}x-1\le2x-3\\3x< x+5\\5-3x\le2x-6\end{matrix}\right.\)
h) \(\left\{{}\begin{matrix}2x+\frac{3}{5}>\frac{3\left(2x-7\right)}{3}\\x-\frac{1}{2}< \frac{5\left(3x-1\right)}{2}\end{matrix}\right.\)
j) \(\left\{{}\begin{matrix}\frac{3x+1}{2}-\frac{3-x}{3}\le\frac{x+1}{4}-\frac{2x-1}{3}\\3-\frac{2x+1}{5}>x+\frac{4}{3}\end{matrix}\right.\)
Biểu diễn của bất phương trình
\(\left\{{}\begin{matrix}4x-3y-1< 0\\x+y\ge7\end{matrix}\right.\)
Mn ơi giải giúp em với ạ ! em xin cảm ơn ạ
Biểu diễn hình học tập nghiệm của các bất phương trình bậc nhất hai ẩn sau :
a. \(-x+2+2\left(y-2\right)< 2\left(1-x\right)\)
b. \(3\left(x-1\right)+4\left(y-2\right)< 5x-3\)
giải hệ
\(\left\{{}\begin{matrix}\frac{1}{x}+\frac{1}{y}=9\\\left(\frac{1}{\sqrt[3]{x}}+\frac{1}{\sqrt[3]{y}}\right)\left(1+\frac{1}{\sqrt[3]{x}}\right)\left(1+\frac{1}{\sqrt[3]{y}}\right)=18\end{matrix}\right.\)
Biểu diễn hình học tập nghiệm của các bất phương trình sau :
a) \(3+2y>0\)
b) \(2x-1< 0\)
c) \(x-5y< 2\)
d) \(2x+y>1\)
e) \(-3x+y+2\le0\)
f) \(2x-3y+5\ge0\)
giải các bất phương trình sau:
a, \(\left|\dfrac{3x+4}{x-2}\right|\le3\)
b, \(\left|\dfrac{2x-3}{x-3}\right|\ge1\)
c, \(4x^2+4x-\left|2x+1\right|\ge5\)
d, \(\left|x^2-5x+4\right|\le x^2+6x+5\)
e, \(x+5>\left|x^2+4x-12\right|\)