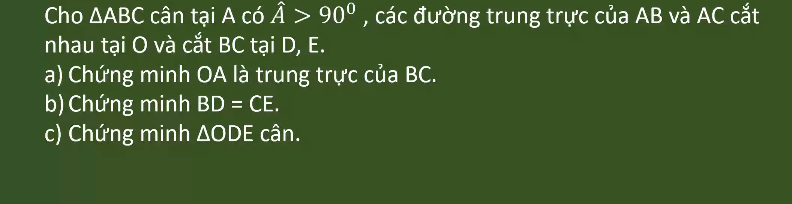cần gấp ai giúp em vs ạ 

Cho hai điểm A, D nằm trên đường trung trực của BC sao cho A, D thuộc hai nửa mặt phẳng đối nhau bờ BC.

a)     Chứng minh ∆ABD = ∆ACD.

b)    Trên AB, AC lấy lần lượt lấy các điểm E, F sao cho AE = AF. Gọi I là giao điểm của BF và CE. Chứng minh A, I, D thẳng hàng.

Bài 1: Cho ∆ABC vuông tại A, biết BC = 10cm, AB = 6cm. Tia phân giác của góc B cắt cạnh AC tại E. Từ E kẻ ED vuông góc với BC tại D.

a)     Tính AC.

b)    Chứng minh ∆ABE = ∆DBE.

c)     Chứng minh BE là đường trung trực của AD.

d)    Kẻ AH ꓕ BC . Chứng minh AD là phân giác của .HAC

Bài 2: Cho ∆ABC vuông tại A. Các đường phân giác của góc B và C cắt nhau tại I. Kẻ IH ꓕ BC . Biết HI = 1cm, HB = 2cm, HC = 3cm. tính chu vi của ∆ABC.