Tâm và bán kính đường tròn đi qua cả 4 đỉnh của hình vuông \(ABCD\) cạnh \(a\) là
Tâm là điểm \(A\) và bán kính là \(R=a\sqrt{2}\).Tâm là giao điểm 2 đường chéo và \(R=a\sqrt{2}\).Tâm là giao điểm 2 đường chéo và \(R=\dfrac{a\sqrt{2}}{2}\).Tâm là điểm \(A\) và bán kính là \(R=\dfrac{a\sqrt{2}}{2}\).Hướng dẫn giải: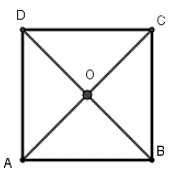
Gọi \(O\) là giao điểm 2 đường chéo \(AC,BD\).
Theo tính chất của hình vuông, ta có: \(OA=OB=OC=OD\) nên \(O\) là tâm đường tròn đi qua cả 4 đỉnh của hình vuông \(ABCD\).
Áp dụng định lí Pytago: \(AC^2=AB^2+BC^2=a^2+a^2=2a^2\)
\(\Rightarrow AC=a\sqrt{2}\Rightarrow OA=OB=OC=OD=R=\dfrac{a\sqrt{2}}{2}\).
