Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số liệt kê phía dưới. Hỏi hàm số đó là hàm số nào?
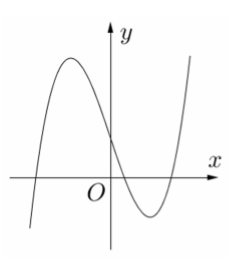
- Hàm số \(y=-x^2+x-1\) có đồ thị là Parabol, không có dạng trên
- Hàm \(y=x^4-x^2+1\) có \(\lim\limits_{x\rightarrow-\infty}y=+\infty\) mà đồ thị cho thấy \(\lim\limits_{x\rightarrow-\infty}=-\infty\), Mâu thuẫn.
- Hàm \(y=-x^3+3x+1\) có \(\lim\limits_{x\rightarrow-\infty}y=+\infty\) mà đồ thị cho thấy \(\lim\limits_{x\rightarrow-\infty}=-\infty\). Mâu thuẫn.
Vậy, bằng phương pháp loại trừ ta thấy chỉ còn hàm \(y=x^3-3x+1\) có thể có đồ thị như hình vẽ.
Chú ý: Giới hạn của đa thức khi \(x\rightarrow\pm\infty\) bằng giới hạn của đơn thức bậc cao nhất. Ví dụ:
\(\lim\limits_{x\rightarrow-\infty}\left(x^4-x^2+1\right)=\lim\limits_{x\rightarrow-\infty}\left(x^4\right)=+\infty\).
