Cho hình lập phương ABCD.A'B'C'D'. Trên cạnh CC' lấy điểm M sao cho \(C'M=2CM.\) Gọi góc tạo bởi \(mp\left(A'D'MM'\right)\) và \(mp\left(ABCD\right)\) là \(\varphi\). Tính giá trị \(cos\varphi\) .
\(\dfrac{3\sqrt{13}}{13}\).\(\dfrac{\sqrt{13}}{13}\).\(\dfrac{2\sqrt{13}}{13}\).\(\dfrac{3}{13}\).Hướng dẫn giải: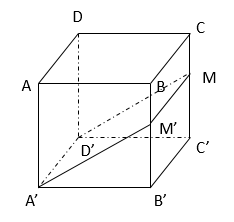
Gọi M' là điểm thuộc BB' sao cho BM' = 2BM'.
Suy ra MM' // B'C' // A'D' hay \(M'\in mp\left(A'D'M\right)\).
Hình chiếu của hình chữ nhật A'D'MM' lên mặt phẳng (ABCD) chính là hình chữ nhật ABCD.
Đặt AB = a. Diện tích hình chữ nhật ABCD là: \(a^2\).
\(C'M=\dfrac{2}{3}a\). Áp dụng định lý Pi-ta-go ta có: \(D'M=\sqrt{\left(D'C'\right)^2+\left(C'M\right)^2}=\sqrt{a^2+\left(\dfrac{2a}{3}\right)^2}=\dfrac{\sqrt{13}}{3}a\).
Diện tích tứ giác A'D'MM' là: \(A'D'.D'M=a.\dfrac{\sqrt{13}a}{3}=\dfrac{\sqrt{13}}{3}a^2\).
Gọi \(\varphi\) là góc tạo bởi mp(A'D'MM') với mp(ABCD).
Suy ra \(S_{ABCD}=cos\varphi.S_{A'D'MM'}\Leftrightarrow cos\varphi=\dfrac{S_{ABCD}}{S_{A'D'MM'}}=\)\(\dfrac{3\sqrt{13}}{13}\).
