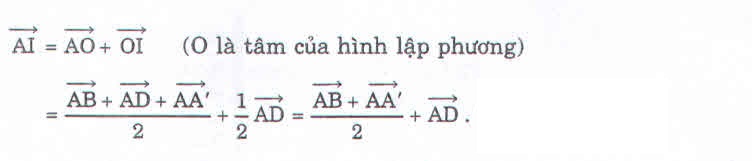
Cho hình lập phương ABCD.A'B'C'D'. Gọi I là tâm của mặt CDD'C'. Tìm hệ thức liên quan giữa \(\overrightarrow{AI}\) với các vectơ \(\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{AA'}\) .
\(\overrightarrow{AI}=\dfrac{\overrightarrow{AB}+\overrightarrow{AA'}}{2}+\overrightarrow{AD}\).\(\overrightarrow{AI}=\dfrac{\overrightarrow{AB}+\overrightarrow{AD}}{2}+\overrightarrow{AA'}\).\(\overrightarrow{AI}=\dfrac{\overrightarrow{AA'}+\overrightarrow{AD}}{2}+\overrightarrow{AB}\).\(\overrightarrow{AI}=\dfrac{\overrightarrow{AB}+\overrightarrow{AA'}+AD}{2}\).Hướng dẫn giải: