Cho hình chóp S.ABCD có SA vuông góc với mp(ABCD), tứ giác ABCD là hình chữ nhật, SA = 3cm, AD = 8cm.Gọi G là trọng tâm tam giác ABC, O là giao điểm của AC và BD. Khoảng cách OG và AB bằng
\(2,4cm\).\(3cm\).\(4cm\).\(2,6cm\).Hướng dẫn giải: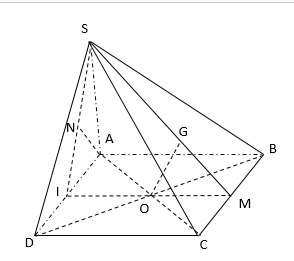
Gọi I, M lần lượt là trung điểm của AD và BC, suy ra \(OG\subset mp\left(SIM\right)\).
Do IM // AB nên AB // mp(SIM). Vì vậy khoảng cách giữa AB và OG bằng khoảng cách từ A đến mp(SIM).
Có IM vuông góc với AD và SA vuông góc với IM nên IM vuông góc với mp(SAD).
Trong mp(SAD) hạ \(AN\perp SI\), suy ra \(AN\perp mp\left(SIM\right)\), vì vậy khoảng cách từ A đến mp(SIM) đến mp(SIM) bằng AN.
AI = AD : 2 = 4(cm).
Áp dụng hệ thức lượng trong tam giác vuông ta có:
\(\dfrac{1}{AN^2}=\dfrac{1}{SA^2}+\dfrac{1}{AI^2}=\dfrac{1}{3^2}+\dfrac{1}{4^2}=\dfrac{25}{144}\).
Suy ra \(AN=2,4\left(cm\right)\).
