Cho hàm số \(y=x^4-4x^2+3\). Phương trình \(\left|x^4-4x^2+3\right|=m\) có bốn nghiệm phân biệt khi và chỉ khi
\(m=0;1< m< 3\). \(m=0\). \(\dfrac{1}{3}< m< 1\). \(m=0;\dfrac{1}{3}< m< 1\). Hướng dẫn giải:Ta khảo sát và vẽ đồ thị hàm số y và hàm |y|
\(y'=4x^3-8x=4x\left(x^2-2\right)=4x\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)\)
y' = 0 tại 3 giá trị của x là \(-\sqrt{2};0;\sqrt{2}\). Lập bảng biến thiên của y:
Vẽ đồ thi hàm y, sau đó lấy đối xứng qua trục hoành phần đồ thị dưới trục hoành thì ta được hàm |y| như hình vẽ dưới đây.
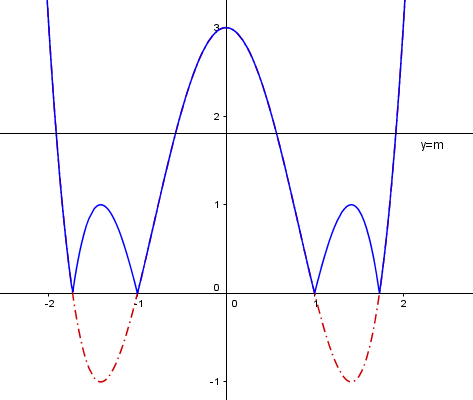
Để đồ thị hàm số \(y=\left|x^4-4x^2+3\right|\) và đường thẳng \(y=m\) cắt nhau tại 4 điểm thì m = 0 hoặc 1 < m < 3
