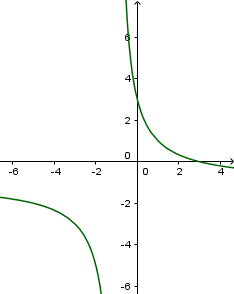
Cho hàm số \(y=\frac{-x+3}{x+1}\). Trong các khẳng định sau, khẳng định nào đúng?
Hàm số đồng biến trên mỗi khoảng \(\left(-\infty;-1\right)\) và \(\left(-1;+\infty\right)\). Hàm số nghịch biến trên mỗi khoảng \(\left(-\infty;-1\right)\) và \(\left(-1;+\infty\right)\). Hàm số nghịch biến trên tập \(\mathbb{R}\backslash\left\{1\right\}\). Hàm số nghịch biến với mọi \(x\ne-1\). Hướng dẫn giải: \(y'=\frac{-4}{\left(x+1\right)^2}< 0,\forall x\ne-1\)
Vậy hàm số đồng biến trên mỗi khoảng xác định của nó.
Chú ý: không thể nói hàm số đồng biến trên tập \(\mathbb{R}\backslash\left\{1\right\}\) được vì đường x = -1 là tiệm cận đứng, lấy 1 điểm \(x_1\) thuộc \(\left(-\infty;-1\right)\) và điểm \(x_2\) thuộc \(\left(-1;+\infty\right)\) thì \(f\left(x_1\right)< f\left(x_2\right)\)