Cho hàm số \(y=f\left(x\right)\) xác định trên \(\mathbb{R}\backslash\left\{0\right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
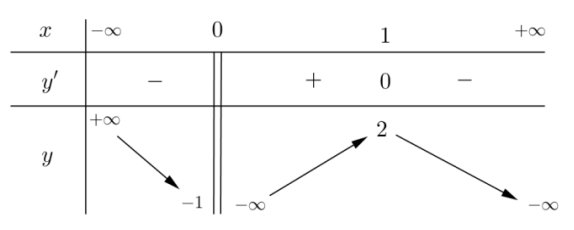
Tập hợp tất cả các giá trị của tham số thực \(m\) sao cho phương trình \(f\left(x\right)=m\) có ba nghiệm thực phân biệt là
\(\left[-1;2\right]\).\(\left(-1;2\right)\).(\(-1;2\)].(\(-\infty;2\)].Hướng dẫn giải:Dựa vào bảng biến thiên thì đường thẳng \(y=m\) cắt đồ thị hàm số tại 3 điểm phân biệt khi: \(-1< m< 2\).
