Cho hàm số \(y=ax^3+bx^2+cx+d\) có đồ thị như hình dưới đây.
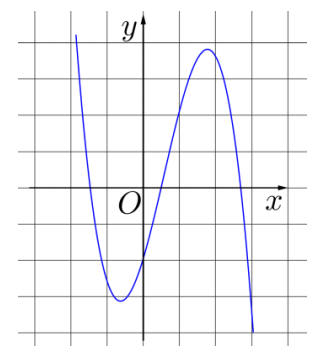
Mệnh đề nào sau đây đúng?
\(a< 0,b>0,c>0,d< 0\).\(a< 0,b< 0,c>0,d< 0\).\(a>0,b< 0,c< 0,d>0\).\(a< 0,b>0,c< 0,d< 0\).Hướng dẫn giải:- Đồ thị cắt trục tung tại điểm có tung độ âm nên \(d=y\left(0\right)< 0.\)
- Nhìn vào đồ thị ta thấy \(\lim\limits_{x\rightarrow-\infty}y=+\infty,\lim\limits_{x\rightarrow+\infty}=-\infty\) nên suy ra \(a< 0\) (vì \(\lim\limits_{x\rightarrow+\infty}\left(ax^3+bx^2+cx+d\right)=\lim\limits_{x\rightarrow+\infty}ax^3=-\infty\) khi và chỉ khi \(a< 0\))
- Đồ thị có 2 điểm cực trị nằm về hai phía của trục tung nên hoành độ hai điểm cực trị trái dấu nhau. Vậy \(y'=3ax^2+2bx+c\) có hai nghiệm \(x_1< 0< x_2\) trái dấu, suy ra \(\dfrac{c}{3a}< 0\) mà \(a< 0\Rightarrow c>0\).
-Ta nhận thấy \(x_1+x_2>0\) (vì \(x_2\) cách xa \(0\) hơn \(x_1\)) nên \(x_1+x_2=-\dfrac{2b}{3a}>0\), mà \(a< 0\) nên \(b>0\).
Vậy \(a< 0,b>0,c>0,d< 0.\)
