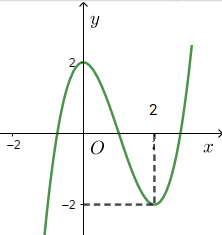
Cho hàm số \(f\left(x\right)=ax^3+bx^2+cx+d\left(a,b,c,d\in\mathbb{R}\right)\). Đồ thị của hàm số \(y=f\left(x\right)\) như hình vẽ ở trên. Số nghiệm thực của phương trình \(3f\left(x\right)+4=0\) là
0.1.2.3.Hướng dẫn giải:Ta có:
\(3f\left(x\right)+4=0\Leftrightarrow f\left(x\right)=-\dfrac{4}{3}\)

Từ đồ thị ta thấy ngay đường thẳng \(y=-\dfrac{4}{3}\) cắt đồ thị tại 3 điểm nên phương trình có 3 nghiệm.
